| Latest Maths NCERT Books Solution | ||||||
|---|---|---|---|---|---|---|
| 6th | 7th | 8th | 9th | 10th | 11th | 12th |
Chapter 7 Fractions
This solutions page provides comprehensive guidance for Chapter 7, "Fractions," a fundamental topic within the Class 6 Ganita Prakash textbook mandated by NCERT for the 2024-25 academic session. Fractions represent a crucial step beyond whole numbers, introducing the concept of parts of a whole or elements within a collection. Mastering fractions is essential for building a robust mathematical foundation. These solutions are meticulously designed to demystify fractional concepts and operations, offering clear, step-by-step explanations for every exercise presented in the chapter.
The journey begins with understanding the very essence of a fraction. The solutions vividly illustrate how fractions, typically written in the form $\frac{a}{b}$ where $b \neq 0$, represent a portion. This is often visualized using diagrams, such as shaded parts of a circle or rectangle, reinforcing the idea of a fraction as 'parts out of a total number of equal parts'. Furthermore, the solutions demonstrate how fractions find their place on the number line, nestled between whole numbers, helping students visualize their magnitude and order relative to integers and other fractions. Accurate representation, both visually and numerically, is emphasized as the first step towards confidence with fractions.
Understanding the different types of fractions is critical. The solutions clearly differentiate between:
- Proper Fractions: Where the numerator is smaller than the denominator (i.e., $\text{numerator} < \text{denominator}$), representing a quantity less than one whole, like $\frac{3}{5}$.
- Improper Fractions: Where the numerator is greater than or equal to the denominator (i.e., $\text{numerator} \ge \text{denominator}$), representing a quantity equal to or greater than one whole, such as $\frac{7}{4}$ or $\frac{5}{5}$.
- Mixed Numbers (or Mixed Fractions): Which combine a whole number and a proper fraction, like $2\frac{1}{3}$.
A significant focus is placed on the concept of equivalent fractions – different fractions that represent the same value (e.g., $\frac{1}{2} = \frac{2}{4} = \frac{3}{6}$). The solutions demonstrate the principle that multiplying or dividing both the numerator and the denominator of a fraction by the same non-zero number results in an equivalent fraction. Related to this is the essential skill of simplifying fractions to their lowest terms or simplest form. This is achieved by dividing both the numerator and the denominator by their Highest Common Factor (HCF), and the solutions illustrate this process clearly.
Comparing and ordering fractions is another vital skill addressed thoroughly. The solutions present robust strategies for determining which fraction is larger or smaller. For unlike fractions (fractions with different denominators), the primary method involves finding a common denominator, typically the Lowest Common Multiple (LCM) of the original denominators. Each fraction is then converted into an equivalent fraction with this common denominator, allowing for direct comparison of the numerators. The alternative method of cross-multiplication is also often explained. Accurate comparison is fundamental for ordering a set of fractions.
Finally, the solutions provide meticulous, step-by-step procedures for performing arithmetic operations: addition and subtraction of fractions. For like fractions (same denominator), the process is straightforward: add or subtract the numerators and keep the common denominator (e.g., $\frac{a}{c} + \frac{b}{c} = \frac{a+b}{c}$). For unlike fractions, the solutions reiterate finding the $\text{LCM}$ of the denominators, converting to equivalent fractions with that $\text{LCM}$ as the new denominator, and then performing the operation on the numerators (e.g., finding $\frac{a}{b} + \frac{c}{d}$ requires finding $\text{LCM}(b,d)$). Operations involving mixed numbers are also carefully explained, usually by converting them to improper fractions first. By diligently working through these solutions for Chapter 7 of the Class 6 Ganita Prakash (NCERT 2024-25), students will gain the necessary skills and confidence to handle fractions effectively, preparing them for subsequent mathematical challenges in algebra and beyond.
Figure it Out (Page 152 - 153)
Fill in the blanks with fractions.
Question 1. Three guavas together weigh 1 kg. If they are roughly of the same size, each guava will roughly weigh ____kg.
Answer:
Given:
Total weight of 3 guavas = $1 \text{ kg}$.
The guavas are roughly of the same size, meaning they have roughly equal weight.
To Find:
The weight of each guava.
Solution:
Since the total weight of 3 guavas is $1 \text{ kg}$ and they have roughly equal weight, the weight of each guava is obtained by dividing the total weight by the number of guavas.
Weight of each guava = $\frac{\text{Total weight}}{\text{Number of guavas}}$
... (1)
Weight of each guava = $\frac{1 \text{ kg}}{3}$
... (2)
Weight of each guava = $\frac{1}{3} \text{ kg}$
... (3)
Answer:
Each guava will roughly weigh $\mathbf{\frac{1}{3}}\text{ kg}$.
Question 2. A wholesale merchant packed 1 kg of rice in four packets of equal weight. The weight of each packet is ___ kg.
Answer:
Given:
Total weight of rice packed = $1 \text{ kg}$.
Number of packets = $4$.
The packets are of equal weight.
To Find:
The weight of each packet.
Solution:
Since the total weight of rice is $1 \text{ kg}$ and it is packed into 4 packets of equal weight, the weight of each packet is obtained by dividing the total weight by the number of packets.
Weight of each packet = $\frac{\text{Total weight}}{\text{Number of packets}}$
... (1)
Weight of each packet = $\frac{1 \text{ kg}}{4}$
... (2)
Weight of each packet = $\frac{1}{4} \text{ kg}$
... (3)
Answer:
The weight of each packet is $\mathbf{\frac{1}{4}}\text{ kg}$.
Question 3. Four friends ordered 3 glasses of sugarcane juice and shared it equally among themselves. Each one drank ____ glass of sugarcane juice
Answer:
Given:
Number of glasses of sugarcane juice = $3$.
Number of friends = $4$.
The juice is shared equally among the friends.
To Find:
The fraction of a glass of sugarcane juice each friend drank.
Solution:
Since the total amount of juice (3 glasses) is shared equally among 4 friends, each friend gets the total amount divided by the number of friends.
Amount of juice per friend = $\frac{\text{Total glasses of juice}}{\text{Number of friends}}$
... (1)
Amount of juice per friend = $\frac{3}{4} \text{ glasses}$
... (2)
Answer:
Each one drank $\mathbf{\frac{3}{4}}$ glass of sugarcane juice.
Question 4.
The big fish weighs $\frac{1}{2}$ kg. The small one weighs $\frac{1}{4}$ kg. Together they weigh ____ kg.
Find out and discuss the words for fractions that are used in the
different languages spoken in your home, city, or state. Ask your
grandparents, parents, teachers, and classmates what words they use
for different fractions, such as for one and a half, three quarters, one
and a quarter, half, quarter, and two and a half, and write them here:
Answer:
Given:
Weight of the big fish = $\frac{1}{2} \text{ kg}$.
Weight of the small fish = $\frac{1}{4} \text{ kg}$.
To Find:
The combined weight of the two fish.
Solution:
To find the combined weight, we need to add the weight of the big fish and the weight of the small fish.
Combined weight = Weight of big fish + Weight of small fish
... (1)
Combined weight = $\frac{1}{2} \text{ kg} + \frac{1}{4} \text{ kg}$
... (2)
To add fractions, they must have a common denominator. The least common multiple of 2 and 4 is 4.
We convert $\frac{1}{2}$ to an equivalent fraction with a denominator of 4:
$\frac{1}{2} = \frac{1 \times 2}{2 \times 2} = \frac{2}{4}$
... (3)
Now, add the fractions:
Combined weight = $\frac{2}{4} \text{ kg} + \frac{1}{4} \text{ kg}$
... (4)
Combined weight = $\frac{2+1}{4} \text{ kg}$
... (5)
Combined weight = $\frac{3}{4} \text{ kg}$
... (6)
Answer (First Part):
Together they weigh $\mathbf{\frac{3}{4}}\text{ kg}$.
Answer (Second Part - Language/Fraction Words):
This part of the question asks you to research and list the words used for different fractions in the languages spoken in your home, city, or state.
This requires gathering information from your grandparents, parents, teachers, and classmates.
Since the answer depends on your specific location and the languages spoken there, I cannot provide a universal answer. Please consult with people in your local community as suggested in the question and write down the fraction words you find in your book.
Question 5.
Arrange these fraction words in order of size from the smallest to the biggest in the empty box below:
One and a half, three quarters, one and a quarter, half, quarter, two and a half.
Answer:
Given:
The fraction words: One and a half, three quarters, one and a quarter, half, quarter, two and a half.
To Arrange:
The fraction words in order of size from smallest to biggest.
Solution:
First, let's represent each fraction word as a numerical value:
- Quarter = $\frac{1}{4}$
- Half = $\frac{1}{2}$
- Three quarters = $\frac{3}{4}$
- One and a quarter = $1 \frac{1}{4}$
- One and a half = $1 \frac{1}{2}$
- Two and a half = $2 \frac{1}{2}$
Now, let's convert the mixed numbers to improper fractions or decimals for easier comparison:
- Quarter = $\frac{1}{4} = 0.25$
- Half = $\frac{1}{2} = 0.5$
- Three quarters = $\frac{3}{4} = 0.75$
- One and a quarter = $1 \frac{1}{4} = \frac{4 \times 1 + 1}{4} = \frac{5}{4} = 1.25$
- One and a half = $1 \frac{1}{2} = \frac{2 \times 1 + 1}{2} = \frac{3}{2} = 1.5$
- Two and a half = $2 \frac{1}{2} = \frac{2 \times 2 + 1}{2} = \frac{5}{2} = 2.5$
Comparing the numerical values: $0.25, 0.5, 0.75, 1.25, 1.5, 2.5$.
Arranging these values from smallest to biggest, we get:
$\frac{1}{4} < \frac{1}{2} < \frac{3}{4} < 1 \frac{1}{4} < 1 \frac{1}{2} < 2 \frac{1}{2}$
... (1)
$0.25 < 0.5 < 0.75 < 1.25 < 1.5 < 2.5$
... (2)
Now, convert the values back to their original fraction words in the sorted order.
Answer:
The fraction words in order of size from the smallest to the biggest are:
Quarter, Half, Three quarters, One and a quarter, One and a half, Two and a half.
Intext Question (Page 154 - 155)
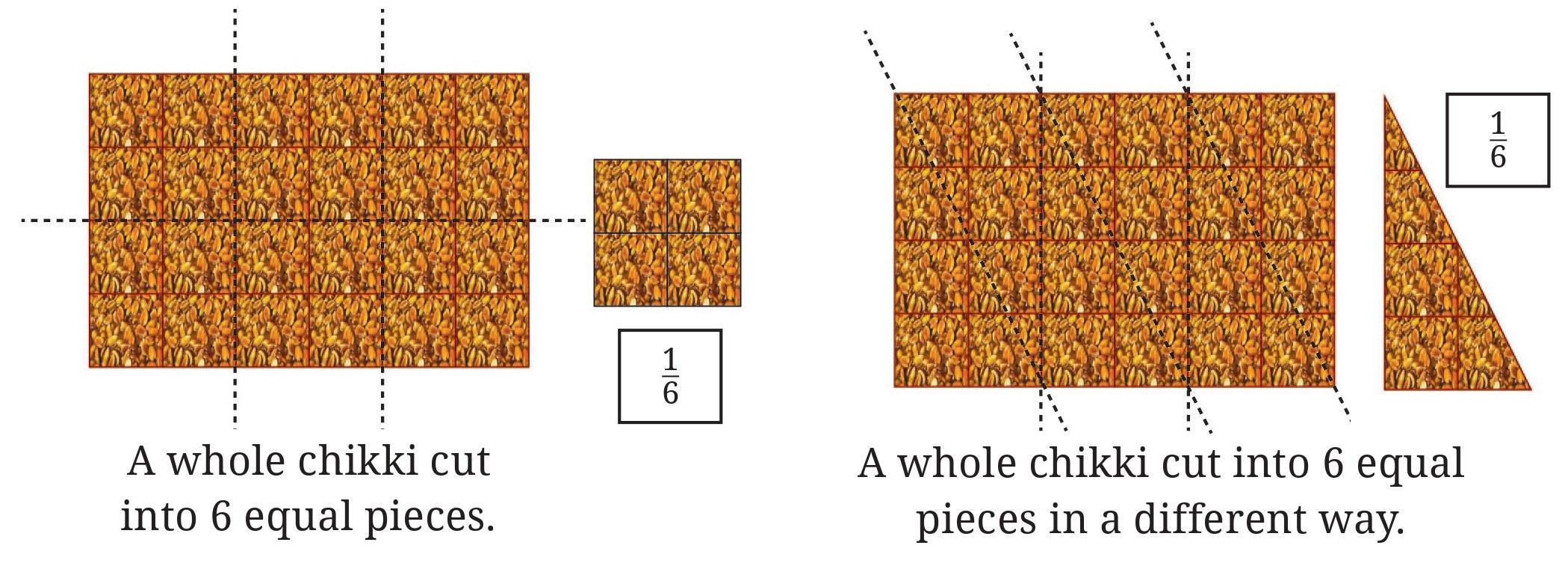
Answer:
Given:
A whole chikki is divided into 6 equal parts in different ways.
This results in $\frac{1}{6}$ chikki pieces of different shapes.
To Determine:
If the $\frac{1}{6}$ chikki pieces of different shapes are of the same size.
Solution:
The question states that the whole chikki is divided into 6 equal parts.
The term "equal parts" in the context of dividing a whole object refers to parts that have the same measure, such as area, volume, or weight.
In this case, when we divide the chikki into 6 equal parts, each part contains the same amount of chikki, which means they have the same area (assuming uniform thickness).
The fraction $\frac{1}{6}$ represents one out of six equal parts of the whole.
While the shapes of the pieces can be different when the chikki is divided in different ways, the size (area) of each piece remains the same because they are defined as "equal parts".
Answer:
Yes, they are of the $\mathbf{same\ size}$.
Dividing a whole into equal parts guarantees that each part has the same measure (area in this case), regardless of its shape.
Figure it Out (Page 155)
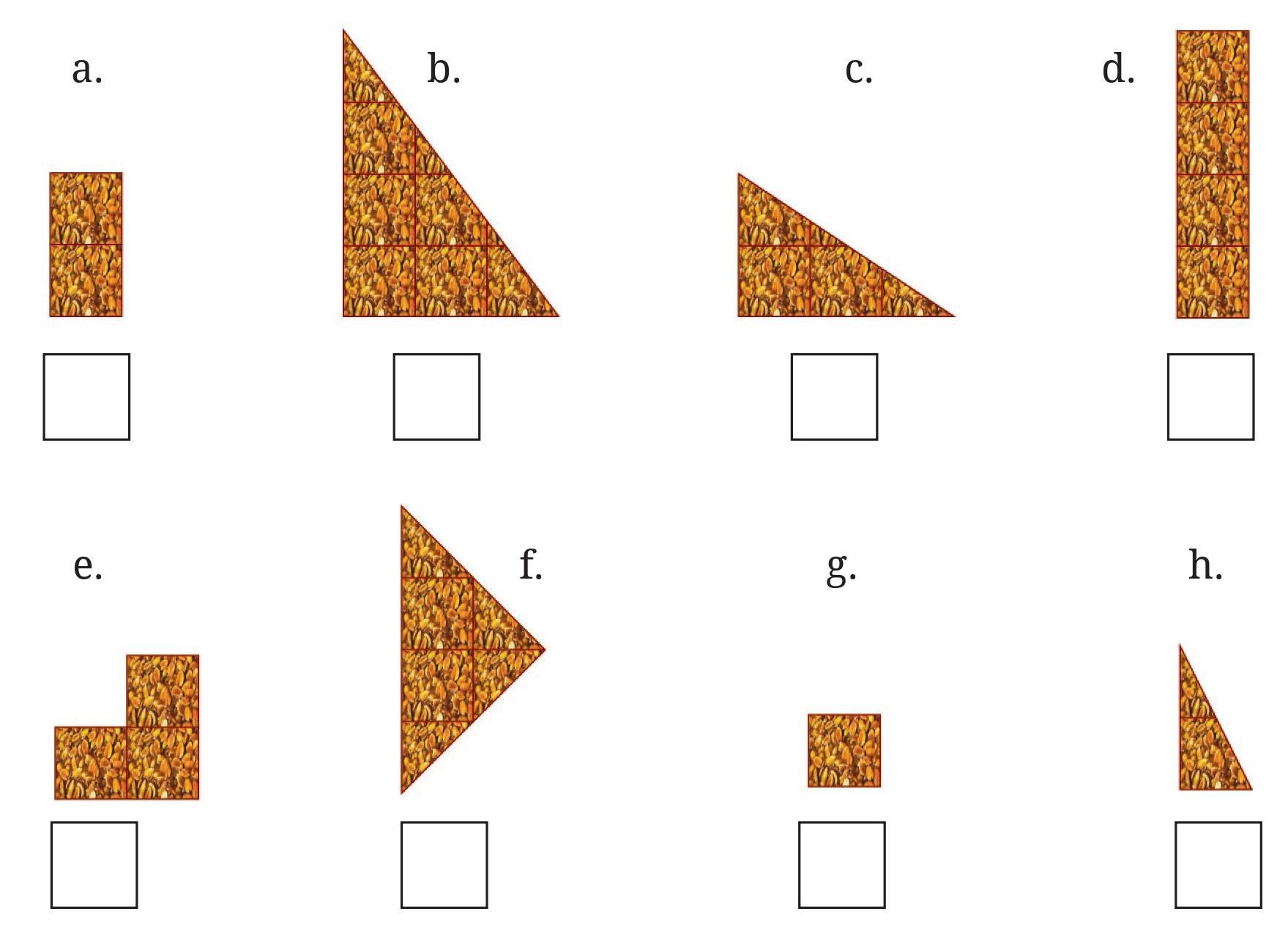
Answer:
Given:
Figures showing a whole chikki divided into different numbers of equal parts.
To Find:
The fractional part of the whole chikki that each piece represents in each figure.
Solution:
The fraction representing a part of a whole is given by $\frac{\text{Number of selected parts}}{\text{Total number of equal parts}}$.
In this case, we are looking at the size of a single piece, so the number of selected parts is 1.
We need to examine each figure to find the total number of equal parts the whole chikki is divided into.
Figure 1:
The chikki is divided into 2 equal parts.
The total number of equal parts is 2.
Each piece represents $\frac{1}{2}$ of the whole chikki.
Figure 2:
The chikki is divided into 3 equal parts.
The total number of equal parts is 3.
Each piece represents $\frac{1}{3}$ of the whole chikki.
Figure 3:
The chikki is divided into 4 equal parts.
The total number of equal parts is 4.
Each piece represents $\frac{1}{4}$ of the whole chikki.
Figure 4:
The chikki is divided into 5 equal parts.
The total number of equal parts is 5.
Each piece represents $\frac{1}{5}$ of the whole chikki.
Figure 5:
The chikki is divided into 6 equal parts.
The total number of equal parts is 6.
Each piece represents $\frac{1}{6}$ of the whole chikki.
Answer:
The fractional part of a whole chikki that each piece represents in the figures are:
Figure 1: $\mathbf{\frac{1}{2}}$
Figure 2: $\mathbf{\frac{1}{3}}$
Figure 3: $\mathbf{\frac{1}{4}}$
Figure 4: $\mathbf{\frac{1}{5}}$
Figure 5: $\mathbf{\frac{1}{6}}$
Figure it Out (Page 158)
Question 1. Continue this table of $\frac{1}{2}$ for 2 more steps.
Answer:
Given:
The task is to continue a table of equivalent fractions for $\frac{1}{2}$ for two more steps.
The table likely shows equivalent fractions generated by multiplying the numerator and the denominator by the same integer.
To Find:
The next two equivalent fractions for $\frac{1}{2}$.
Solution:
Equivalent fractions are obtained by multiplying the numerator and the denominator of a fraction by the same non-zero number.
The standard method to generate a sequence of equivalent fractions for $\frac{1}{2}$ is by multiplying the numerator and denominator by consecutive integers (1, 2, 3, 4, 5, ...).
The table would typically start like this:
$\frac{1}{2} = \frac{1 \times 1}{2 \times 1} = \frac{1}{2}$
$\frac{1}{2} = \frac{1 \times 2}{2 \times 2} = \frac{2}{4}$
$\frac{1}{2} = \frac{1 \times 3}{2 \times 3} = \frac{3}{6}$
To continue the table for 2 more steps, we multiply the numerator and denominator by the next consecutive integers, which are 4 and 5.
Step 1 (Multiplying by 4):
$\frac{1}{2} = \frac{1 \times 4}{2 \times 4} = \frac{4}{8}$
... (1)
Step 2 (Multiplying by 5):
$\frac{1}{2} = \frac{1 \times 5}{2 \times 5} = \frac{5}{10}$
... (2)
Answer:
Continuing the table of $\frac{1}{2}$ for 2 more steps, we get the equivalent fractions $\mathbf{\frac{4}{8}}$ and $\mathbf{\frac{5}{10}}$.
The table would continue as:
$\frac{1}{2} = \frac{1}{2} = \frac{2}{4} = \frac{3}{6} = \mathbf{\frac{4}{8}} = \mathbf{\frac{5}{10}} = \dots$
Question 2. Can you create a similar table for $\frac{1}{4}$?
Answer:
Given:
The request is to create a table of equivalent fractions for $\frac{1}{4}$.
To Create:
A table showing equivalent fractions for $\frac{1}{4}$.
Solution:
Equivalent fractions for $\frac{1}{4}$ can be generated by multiplying the numerator (1) and the denominator (4) by the same non-zero integer.
Let's multiply by consecutive integers (2, 3, 4, 5, ...) to create the table.
Multiplying by 2:
$\frac{1}{4} = \frac{1 \times 2}{4 \times 2} = \frac{2}{8}$
... (1)
Multiplying by 3:
$\frac{1}{4} = \frac{1 \times 3}{4 \times 3} = \frac{3}{12}$
... (2)
Multiplying by 4:
$\frac{1}{4} = \frac{1 \times 4}{4 \times 4} = \frac{4}{16}$
... (3)
Multiplying by 5:
$\frac{1}{4} = \frac{1 \times 5}{4 \times 5} = \frac{5}{20}$
... (4)
We can list these equivalent fractions to form a table.
Answer:
A table for $\frac{1}{4}$ can be created as follows:
$\frac{1}{4} = \frac{2}{8} = \frac{3}{12} = \frac{4}{16} = \frac{5}{20} = \frac{6}{24} = \dots$
Each fraction in this sequence is equivalent to $\frac{1}{4}$.
Question 3. Make $\frac{1}{3}$ using a paper strip. Can you use this to also make $\frac{1}{6}$?
Answer:
Given:
A paper strip.
To Do:
Make the fraction $\frac{1}{3}$ using the paper strip.
Determine if this method can be used to also make $\frac{1}{6}$.
Solution (Making $\frac{1}{3}$):
1. Take a rectangular paper strip.
2. To make $\frac{1}{3}$, you need to divide the strip into 3 equal parts. One way to do this is by folding.
3. Fold the strip roughly into three parts that appear equal. Adjust the folds until the three sections are as close to equal in length as possible when unfolded.
4. Once folded and unfolded, the strip will have creases that divide it into 3 roughly equal sections. Each section represents $\frac{1}{3}$ of the whole strip.
5. You can draw lines along the creases to mark the divisions clearly.
Solution (Making $\frac{1}{6}$):
Yes, you can use the paper strip that is already divided into thirds to make $\frac{1}{6}$.
1. The strip is already divided into 3 equal parts, each representing $\frac{1}{3}$.
2. To get $\frac{1}{6}$ of the whole strip, you need to divide the entire strip into 6 equal parts.
3. Since the strip is in three $\frac{1}{3}$ sections, you can fold the strip in half along its length. This fold will divide each of the existing $\frac{1}{3}$ sections into two equal smaller sections.
4. When you unfold the strip, you will have $3 \times 2 = 6$ equal sections.
5. Each of these new, smaller sections represents $\frac{1}{6}$ of the original whole strip because you have divided the whole into 6 equal parts.
Answer:
You can make $\frac{1}{3}$ by folding the paper strip into three equal parts.
Yes, you can use this strip (divided into thirds) to also make $\frac{1}{6}$. By folding the strip in half along its length, you divide each third into two smaller equal parts, resulting in six equal parts of the whole strip, where each part is $\frac{1}{6}$.
Question 4. Draw a picture and write an addition statement as above to show:
a. 5 times $\frac{1}{4}$ of a roti
b. 9 times $\frac{1}{4}$ of a roti
Answer:
Given:
Fractions of a whole roti.
To Do:
Draw a picture and write an addition statement to show the results of multiplying $\frac{1}{4}$ of a roti by 5 and 9.
a. 5 times $\frac{1}{4}$ of a roti
Solution (a):
The phrase "5 times $\frac{1}{4}$" means adding $\frac{1}{4}$ to itself 5 times.
Drawing (Description):
To represent $\frac{1}{4}$ of a roti, draw a circle (representing a whole roti) and divide it into 4 equal parts. Shade or highlight one of these parts.
To represent 5 times $\frac{1}{4}$, you need to show five such $\frac{1}{4}$ parts.
Draw two circles (rotis). Divide each circle into 4 equal parts.
In the first circle, shade or highlight all 4 parts (representing $\frac{4}{4}$ or 1 whole roti).
In the second circle, shade or highlight only 1 part (representing $\frac{1}{4}$ of the second roti).
This drawing visually shows $\frac{4}{4} + \frac{1}{4}$, which is equivalent to five $\frac{1}{4}$ parts taken together.
Addition Statement:
$\frac{1}{4} + \frac{1}{4} + \frac{1}{4} + \frac{1}{4} + \frac{1}{4} = \frac{1+1+1+1+1}{4} = \frac{5}{4}$
... (1)
The improper fraction $\frac{5}{4}$ can be written as a mixed number:
$\frac{5}{4} = 1 \frac{1}{4}$
... (2)
Answer (a):
5 times $\frac{1}{4}$ of a roti is equal to $\mathbf{\frac{5}{4}}$ or $\mathbf{1 \frac{1}{4}}$ rotis.
b. 9 times $\frac{1}{4}$ of a roti
Solution (b):
The phrase "9 times $\frac{1}{4}$" means adding $\frac{1}{4}$ to itself 9 times.
Drawing (Description):
To represent 9 times $\frac{1}{4}$, you need to show nine such $\frac{1}{4}$ parts.
Draw three circles (rotis). Divide each circle into 4 equal parts.
In the first circle, shade or highlight all 4 parts (representing $\frac{4}{4}$ or 1 whole roti).
In the second circle, shade or highlight all 4 parts (representing another $\frac{4}{4}$ or 1 whole roti).
In the third circle, shade or highlight only 1 part (representing $\frac{1}{4}$ of the third roti).
This drawing visually shows $\frac{4}{4} + \frac{4}{4} + \frac{1}{4}$, which is equivalent to nine $\frac{1}{4}$ parts taken together.
Addition Statement:
$\frac{1}{4} + \frac{1}{4} + \frac{1}{4} + \frac{1}{4} + \frac{1}{4} + \frac{1}{4} + \frac{1}{4} + \frac{1}{4} + \frac{1}{4} = \frac{1+1+1+1+1+1+1+1+1}{4} = \frac{9}{4}$
... (3)
The improper fraction $\frac{9}{4}$ can be written as a mixed number:
$\frac{9}{4} = 2 \frac{1}{4}$
... (4)
Answer (b):
9 times $\frac{1}{4}$ of a roti is equal to $\mathbf{\frac{9}{4}}$ or $\mathbf{2 \frac{1}{4}}$ rotis.
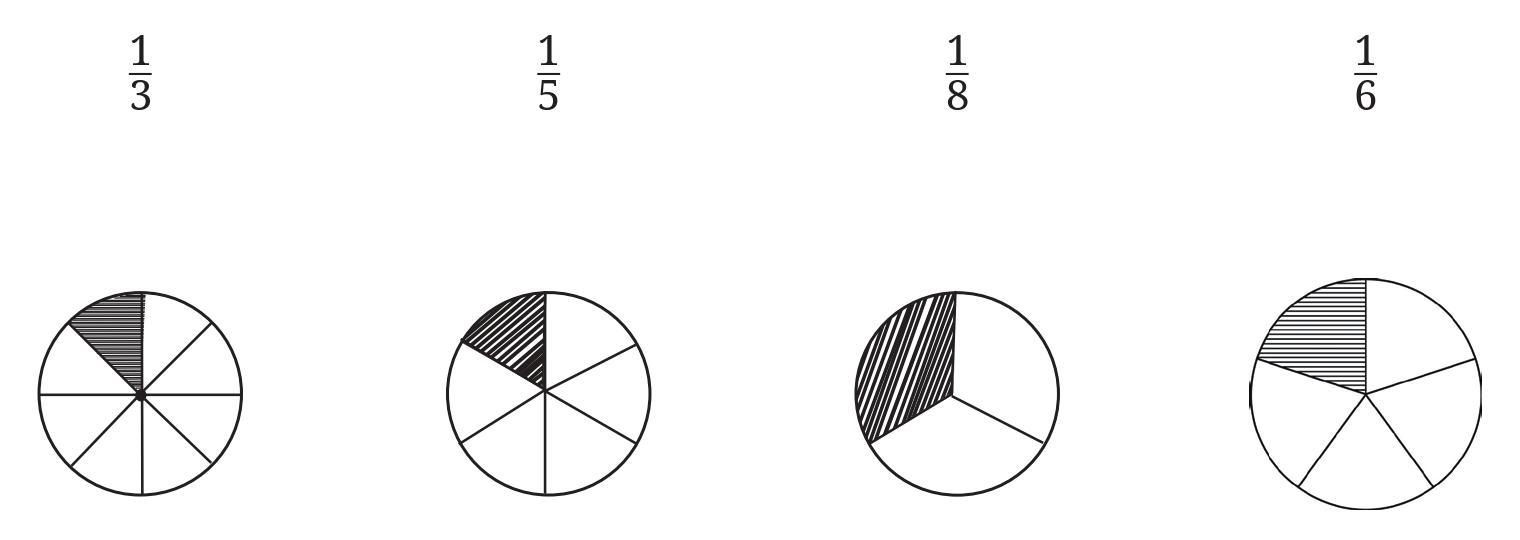
Answer:
Given:
Various fractional units and pictures representing parts of a whole.
To Match:
Each fractional unit with the correct picture.
Solution:
We need to identify the fraction represented by each picture and match it with the corresponding fractional unit.
A fractional unit is represented by $\frac{1}{\text{Total number of equal parts}}$.
Examining the pictures:
- Picture A shows a shape divided into 5 equal parts, with 1 part highlighted. This represents the fractional unit $\frac{1}{5}$.
- Picture B shows a shape divided into 4 equal parts, with 1 part highlighted. This represents the fractional unit $\frac{1}{4}$.
- Picture C shows a shape divided into 2 equal parts, with 1 part highlighted. This represents the fractional unit $\frac{1}{2}$.
- Picture D shows a shape divided into 3 equal parts, with 1 part highlighted. This represents the fractional unit $\frac{1}{3}$.
- Picture E shows a shape divided into 6 equal parts, with 1 part highlighted. This represents the fractional unit $\frac{1}{6}$.
Matching the fractional units with the pictures:
$\frac{1}{2}$ matches Picture C.
$\frac{1}{3}$ matches Picture D.
$\frac{1}{4}$ matches Picture B.
$\frac{1}{5}$ matches Picture A.
$\frac{1}{6}$ matches Picture E.
Intext Question (Page 159)
Question: Now, can you find the lengths of the various blue lines shown below? Fill in the boxes as well.
1. Here, the fractional unit is dividing a length of 1 unit into three equal parts. Write the fraction that gives the length of the blue line in the box or in your notebook.

2. Here, a unit is divided into 5 equal parts. Write the fraction that gives the length of the blue lines in the respective boxes or in your notebook.

3. Now, a unit is divided into 8 equal parts. Write the appropriate fractions in your notebook.
Answer:
We need to find the lengths of the blue lines shown on the number lines by representing them as fractions.
1. Here, the fractional unit is dividing a length of 1 unit into three equal parts. Write the fraction that gives the length of the blue line in the box or in your notebook.
Given:
A unit length is divided into 3 equal parts.
The blue line starts from 0 and extends to the second division mark.
To Find:
The fraction representing the length of the blue line.
Solution:
Since the unit length is divided into 3 equal parts, each part represents $\frac{1}{3}$ of the unit.
The blue line covers 2 of these equal parts, starting from 0.
The length of the blue line is the sum of the lengths of the parts it covers.
Length of blue line = $\frac{1}{3} + \frac{1}{3}$
... (1)
Length of blue line = $\frac{1+1}{3}$
Length of blue line = $\frac{2}{3}$ units
... (2)
This can also be seen directly from the number line: the blue line ends at the second mark out of three total divisions, starting from zero. This represents the fraction $\frac{2}{3}$.
Answer:
The length of the blue line is $\mathbf{\frac{2}{3}}$ of the unit length.
2. Here, a unit is divided into 5 equal parts. Write the fraction that gives the length of the blue lines in the respective boxes or in your notebook.
Given:
A unit length is divided into 5 equal parts.
There are three blue lines, starting from 0, ending at different division marks.
To Find:
The fractions representing the lengths of the three blue lines.
Solution:
Since the unit length is divided into 5 equal parts, each part represents $\frac{1}{5}$ of the unit.
The blue lines start from 0 and end at specific division marks.
The length of a blue line is the number of equal parts it covers, divided by the total number of equal parts in the unit.
Let's look at each blue line:
The first blue line ends at the first division mark from 0. It covers 1 out of 5 equal parts. Its length is $\frac{1}{5}$ units.
The second blue line ends at the third division mark from 0. It covers 3 out of 5 equal parts. Its length is $\frac{3}{5}$ units.
The third blue line ends at the fifth division mark from 0, which is the end of the unit. It covers 5 out of 5 equal parts. Its length is $\frac{5}{5}$ units, which is equal to 1 unit.
Answer:
The lengths of the blue lines are $\mathbf{\frac{1}{5}}$, $\mathbf{\frac{3}{5}}$, and $\mathbf{\frac{5}{5}}$ (or 1) units.
3. Now, a unit is divided into 8 equal parts. Write the appropriate fractions in your notebook.
Given:
A unit length is divided into 8 equal parts.
We need to write the appropriate fractions for the marked points on this number line.
To Find:
The fractions corresponding to each division mark from 0 to 1.
Solution:
Since the unit length is divided into 8 equal parts, each part represents $\frac{1}{8}$ of the unit.
The marks on the number line represent multiples of this fractional unit, starting from 0.
The point at the start (0) represents $\frac{0}{8}$.
The first mark represents 1 part out of 8, which is $\frac{1}{8}$.
The second mark represents 2 parts out of 8, which is $\frac{2}{8}$.
The third mark represents 3 parts out of 8, which is $\frac{3}{8}$.
The fourth mark represents 4 parts out of 8, which is $\frac{4}{8}$.
The fifth mark represents 5 parts out of 8, which is $\frac{5}{8}$.
The sixth mark represents 6 parts out of 8, which is $\frac{6}{8}$.
The seventh mark represents 7 parts out of 8, which is $\frac{7}{8}$.
The eighth mark (at the end of the unit, 1) represents 8 parts out of 8, which is $\frac{8}{8}$ or 1.
Answer:
The appropriate fractions for the division marks when a unit is divided into 8 equal parts are:
$\mathbf{\frac{0}{8}}$, $\mathbf{\frac{1}{8}}$, $\mathbf{\frac{2}{8}}$, $\mathbf{\frac{3}{8}}$, $\mathbf{\frac{4}{8}}$, $\mathbf{\frac{5}{8}}$, $\mathbf{\frac{6}{8}}$, $\mathbf{\frac{7}{8}}$, $\mathbf{\frac{8}{8}}$.
Figure it Out (Page 160)
Question 1. On a number line, draw lines of lengths $\frac{1}{10}$ , $\frac{3}{10}$ , and $\frac{4}{5}$.
Answer:
Given:
Fractions: $\frac{1}{10}$, $\frac{3}{10}$, and $\frac{4}{5}$.
To Do:
Draw a number line and show the lengths corresponding to these fractions.
Solution:
To represent these fractions as lengths on a number line, we first need to decide on the unit length and how to divide it.
The fractions given are $\frac{1}{10}$, $\frac{3}{10}$, and $\frac{4}{5}$.
To easily compare and represent them, we can express all fractions with a common denominator. The denominators are 10 and 5. The least common multiple of 10 and 5 is 10.
Let's convert $\frac{4}{5}$ to an equivalent fraction with a denominator of 10:
$\frac{4}{5} = \frac{4 \times 2}{5 \times 2} = \frac{8}{10}$
... (1)
So, the fractions we need to represent are $\frac{1}{10}$, $\frac{3}{10}$, and $\frac{8}{10}$.
Since the largest denominator is 10, it is convenient to draw a number line from 0 to 1 and divide the unit length (from 0 to 1) into 10 equal parts.
Steps to draw the number line:
1. Draw a straight horizontal line and mark a point as 0 at the left end.
2. Mark another point some distance to the right as 1 (representing the end of the unit length).
3. Divide the segment between 0 and 1 into 10 equal smaller segments. Mark the division points. These marks represent the fractions $\frac{1}{10}, \frac{2}{10}, \frac{3}{10}, \dots, \frac{9}{10}, \frac{10}{10}$ (which is 1).
4. Now, draw blue lines starting from 0 and ending at the points corresponding to the given fractions:
- For $\frac{1}{10}$: Draw a blue line from 0 to the first division mark after 0.
- For $\frac{3}{10}$: Draw a blue line from 0 to the third division mark after 0.
- For $\frac{4}{5}$ (which is $\frac{8}{10}$): Draw a blue line from 0 to the eighth division mark after 0.
Answer (Description of the drawing):
Draw a number line from 0 to 1, divided into 10 equal segments. The marks will be at $\frac{0}{10}, \frac{1}{10}, \frac{2}{10}, \frac{3}{10}, \frac{4}{10}, \frac{5}{10}, \frac{6}{10}, \frac{7}{10}, \frac{8}{10}, \frac{9}{10}, \frac{10}{10}$.
Draw a blue line segment from 0 to the mark $\frac{1}{10}$.
Draw a blue line segment from 0 to the mark $\frac{3}{10}$.
Draw a blue line segment from 0 to the mark $\frac{8}{10}$ (which corresponds to $\frac{4}{5}$).
Question 2. Write five more fractions of your choice and mark them on the number line.
Answer:
Given:
The task is to choose five fractions and mark them on a number line.
To Do:
Choose five fractions and illustrate how to mark them on a number line.
Solution:
Let's choose the following five fractions:
$\frac{1}{2}$, $\frac{2}{3}$, $\frac{5}{4}$, $\frac{7}{8}$, $\frac{11}{5}$
To mark these fractions on a number line, we first draw a line and mark whole number units on it (e.g., 0, 1, 2, 3, ...).
Then, for each fraction, we divide the relevant unit segment(s) into the number of equal parts indicated by the denominator and mark the position indicated by the numerator.
Some of these fractions are greater than 1, so the number line needs to extend beyond 1.
- $\frac{1}{2} = 0.5$
- $\frac{2}{3} \approx 0.67$
- $\frac{5}{4} = 1 \frac{1}{4} = 1.25$
- $\frac{7}{8} = 0.875$
- $\frac{11}{5} = 2 \frac{1}{5} = 2.2$
The fractions range from $\frac{1}{2}$ to $\frac{11}{5}$. We need a number line that goes from 0 up to at least 3.
How to mark each fraction:
1. Draw a number line and mark the points 0, 1, 2, 3.
2. To mark $\mathbf{\frac{1}{2}}$:
Divide the segment between 0 and 1 into 2 equal parts.
Mark the first point from 0. This point is $\frac{1}{2}$.
3. To mark $\mathbf{\frac{2}{3}}$:
Divide the segment between 0 and 1 into 3 equal parts.
Mark the second point from 0. This point is $\frac{2}{3}$.
4. To mark $\mathbf{\frac{5}{4}}$:
Rewrite $\frac{5}{4}$ as a mixed number: $1 \frac{1}{4}$. This means 1 whole unit plus $\frac{1}{4}$ of the next unit.
Go to the point 1 on the number line.
Divide the segment between 1 and 2 into 4 equal parts.
Mark the first point after 1. This point is $1 \frac{1}{4}$ or $\frac{5}{4}$.
5. To mark $\mathbf{\frac{7}{8}}$:
Divide the segment between 0 and 1 into 8 equal parts.
Mark the seventh point from 0. This point is $\frac{7}{8}$.
6. To mark $\mathbf{\frac{11}{5}}$:
Rewrite $\frac{11}{5}$ as a mixed number: $2 \frac{1}{5}$. This means 2 whole units plus $\frac{1}{5}$ of the next unit.
Go to the point 2 on the number line.
Divide the segment between 2 and 3 into 5 equal parts.
Mark the first point after 2. This point is $2 \frac{1}{5}$ or $\frac{11}{5}$.
Answer:
The five chosen fractions are $\frac{1}{2}$, $\frac{2}{3}$, $\frac{5}{4}$, $\frac{7}{8}$, and $\frac{11}{5}$.
A number line showing these fractions would look like this (conceptual drawing description):
Draw a line with points 0, 1, 2, 3 marked at equal intervals.
Mark $\frac{1}{2}$ halfway between 0 and 1.
Mark $\frac{2}{3}$ two-thirds of the way from 0 to 1.
Mark $\frac{7}{8}$ seven-eighths of the way from 0 to 1 (close to 1).
Mark $\frac{5}{4}$ one-fourth of the way between 1 and 2.
Mark $\frac{11}{5}$ one-fifth of the way between 2 and 3.
Question 3. How many fractions lie between 0 and 1? Think, discuss with your classmates, and write your answer.
Answer:
Given:
The question asks about the number of fractions that lie between 0 and 1 on a number line.
To Find:
The count of fractions between 0 and 1.
Solution:
A fraction is a number that can be represented as $\frac{p}{q}$, where $p$ and $q$ are integers and $q \neq 0$. For a fraction to be strictly between 0 and 1, it must satisfy the condition $0 < \frac{p}{q} < 1$. We usually consider positive fractions for this context, so $p > 0$ and $q > 0$. The condition $0 < \frac{p}{q} < 1$ implies $p < q$ (since $q > 0$). So, we are looking for the number of fractions where the numerator is a positive integer less than the denominator, which is also a positive integer.
Let's consider some examples of fractions between 0 and 1:
- With denominator 2: $\frac{1}{2}$
- With denominator 3: $\frac{1}{3}, \frac{2}{3}$
- With denominator 4: $\frac{1}{4}, \frac{2}{4} (\text{which is } \frac{1}{2}), \frac{3}{4}$
- With denominator 5: $\frac{1}{5}, \frac{2}{5}, \frac{3}{5}, \frac{4}{5}$
- With denominator 100: $\frac{1}{100}, \frac{2}{100}, \dots, \frac{99}{100}$ (99 fractions)
For any positive integer $q$, we can form fractions $\frac{p}{q}$ where $p$ is a positive integer and $p < q$. The possible values for $p$ are $1, 2, \dots, q-1$. There are $q-1$ such fractions for a given denominator $q$. As $q$ can be any positive integer greater than 1, there are infinitely many possible denominators ($2, 3, 4, \dots$).
Consider any two distinct fractions between 0 and 1, say $\frac{a}{b}$ and $\frac{c}{d}$, where $0 < \frac{a}{b} < \frac{c}{d} < 1$. We can always find another fraction between them. For instance, consider their average: $\frac{\frac{a}{b} + \frac{c}{d}}{2}$. This average will be a fraction and will lie between $\frac{a}{b}$ and $\frac{c}{d}$. Since we can repeat this process indefinitely, we can find infinitely many distinct fractions between any two distinct fractions, and thus between 0 and 1.
This property means that fractions (rational numbers) are dense on the number line. Between any two distinct points, there is always a fraction.
Answer:
There are infinitely many fractions that lie between 0 and 1.

Answer:
Given:
A number line segment from 0 to 1.
The unit distance between 0 and 1 is divided into two equal parts.
The length of each equal part is $\frac{1}{2}$ unit.
The blue line covers the first part, from 0 to the mark at $\frac{1}{2}$. Its length is $\frac{1}{2}$ unit.
The black line starts from the mark at $\frac{1}{2}$ and extends to the mark at 1.
To Find:
The length of the black line, expressed as a fraction.
Solution:
The unit length from 0 to 1 is divided into two equal parts.
The first equal part is covered by the blue line, starting from 0 and ending at the mark at $\frac{1}{2}$. The length of this part is $\frac{1}{2}$.
The second equal part starts from the mark at $\frac{1}{2}$ and ends at the mark at 1.
The black line covers this second equal part.
Since the unit length is divided into two equal parts, and the black line covers one of these equal parts, the length of the black line is $\frac{1}{2}$ of the unit length.
Alternatively, the length of the black line is the difference between its end point (1) and its starting point ($\frac{1}{2}$).
Length of black line = $1 - \frac{1}{2}$
... (1)
To subtract the fractions, we find a common denominator, which is 2.
$1 = \frac{2}{2}$
... (2)
Length of black line = $\frac{2}{2} - \frac{1}{2}$
... (3)
Length of black line = $\frac{2-1}{2}$
... (4)
Length of black line = $\frac{1}{2}$ units
... (5)
Answer:
The length of the black line is $\mathbf{\frac{1}{2}}$ units.
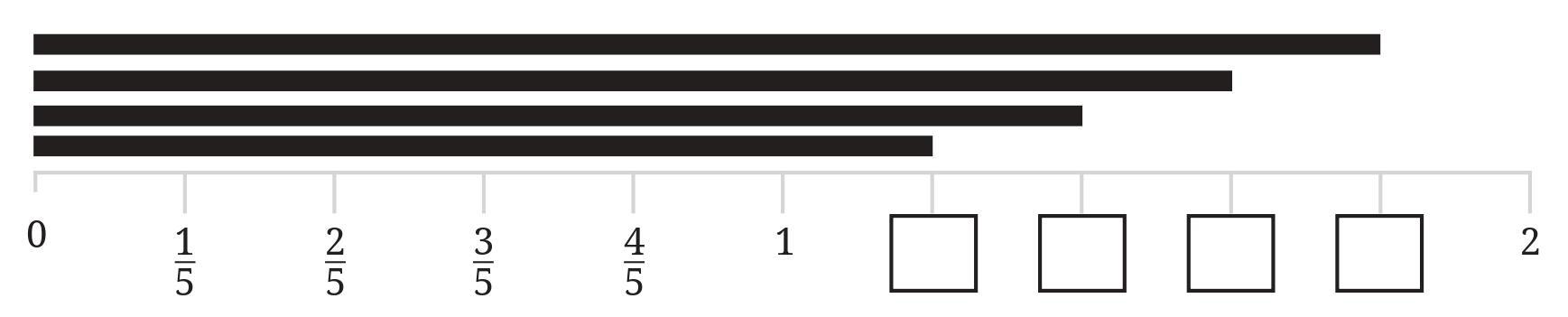
Answer:
Given:
A number line segment from 0 to 1.
The distance between 0 and 1 is 1 unit long.
The unit distance is divided into four equal parts.
There are two black lines shown on the number line.
To Find:
The length of each black line, expressed as a fraction.
Solution:
Since the unit length from 0 to 1 is divided into four equal parts, each part represents $\frac{1}{4}$ of the unit length.
The division marks on the number line correspond to the fractions $\frac{1}{4}, \frac{2}{4}, \frac{3}{4}$, and $\frac{4}{4}$ (which is 1), starting from 0.
Length of the first black line:
The first black line starts at 0 and ends at the first division mark.
The position of the first division mark from 0 is $\frac{1}{4}$.
The length of the first black line is the distance between 0 and $\frac{1}{4}$.
Length$_1 = \frac{1}{4} - 0$
... (1)
Length$_1 = \frac{1}{4}$ units
... (2)
Length of the second black line:
The second black line starts at the second division mark and ends at the third division mark.
The position of the second division mark from 0 is $\frac{2}{4}$.
The position of the third division mark from 0 is $\frac{3}{4}$.
The length of the second black line is the distance between $\frac{2}{4}$ and $\frac{3}{4}$.
Length$_2 = \frac{3}{4} - \frac{2}{4}$
... (3)
Length$_2 = \frac{3-2}{4}$
... (4)
Length$_2 = \frac{1}{4}$ units
... (5)
Both black lines cover exactly one of the four equal segments that make up the unit length.
Answer:
The length of the first black line is $\mathbf{\frac{1}{4}}$ units.
The length of the second black line is $\mathbf{\frac{1}{4}}$ units.
Intext Question (Page 161)
Now, let us classify these in two groups:

Answer:
Based on the fractions we have encountered and marked on number lines in the previous questions, the fractions that are greater than 1 are those where the numerator is larger than the denominator.
Let's recall some of the fractions marked or discussed:
- From Intext Question (Page 159): $\frac{1}{3}, \frac{2}{3}, \frac{1}{5}, \frac{3}{5}, \frac{5}{5} (=1), \frac{0}{8}, \frac{1}{8}, \dots, \frac{8}{8} (=1)$. None of these are strictly greater than 1.
- From Figure it Out (Page 160) Question 1: $\frac{1}{10}, \frac{3}{10}, \frac{4}{5} (=\frac{8}{10})$. None of these are strictly greater than 1.
- From Figure it Out (Page 160) Question 2 (our example fractions): $\frac{1}{2}, \frac{2}{3}, \frac{5}{4}, \frac{7}{8}, \frac{11}{5}$.
From the list in Question 2 (Page 160), the fractions greater than 1 are $\frac{5}{4}$ and $\frac{11}{5}$.
Let's look at these fractions and their numerators and denominators:
- For $\frac{5}{4}$: Numerator is 5, Denominator is 4. Here, $5 > 4$.
- For $\frac{11}{5}$: Numerator is 11, Denominator is 5. Here, $11 > 5$.
In both cases, the numerator is greater than the denominator.
A fraction $\frac{p}{q}$ represents $p$ parts, where the whole is divided into $q$ equal parts. If $p > q$, it means we have more than enough parts to make up one whole (or multiple wholes).
For example, $\frac{5}{4}$ means we have 5 parts, and 4 parts make a whole. So, 5 parts make one whole ($\frac{4}{4}$) and one additional part ($\frac{1}{4}$), totaling $1 \frac{1}{4}$, which is greater than 1.
Similarly, $\frac{11}{5}$ means we have 11 parts, and 5 parts make a whole. So, 11 parts make two wholes ($\frac{5}{5} + \frac{5}{5} = \frac{10}{5}$) and one additional part ($\frac{1}{5}$), totaling $2 \frac{1}{5}$, which is greater than 1.
Answer:
Yes, the common characteristic between the fractions that are greater than 1 is that the numerator is greater than the denominator.
Figure it Out (Page 162)
Question 1. How many whole units are there in $\frac{7}{2}$?
Answer:
Given:
The fraction is $\frac{7}{2}$.
To Find:
The number of whole units in $\frac{7}{2}$.
Solution:
To find the number of whole units in an improper fraction like $\frac{7}{2}$, we can convert it into a mixed number. A mixed number consists of a whole number part and a fractional part.
The fraction $\frac{7}{2}$ means 7 parts, where each whole unit is divided into 2 equal parts. To find how many whole units are formed by these 7 parts, we can divide the total number of parts (numerator) by the number of parts that make up one whole (denominator).
Divide the numerator (7) by the denominator (2):
$7 \div 2$
... (1)
Using division:
$7 = 2 \times 3 + 1$
So, the quotient is 3, and the remainder is 1.
This means $\frac{7}{2}$ can be written as:
$\frac{7}{2} = \frac{2 \times 3 + 1}{2}$
... (2)
$\frac{7}{2} = \frac{2 \times 3}{2} + \frac{1}{2}$
$\frac{7}{2} = 3 + \frac{1}{2}$
... (3)
This is the mixed number form: $3 \frac{1}{2}$.
The whole number part of the mixed number is 3. This indicates the number of whole units in the fraction $\frac{7}{2}$.
Answer:
There are $\mathbf{3}$ whole units in $\frac{7}{2}$.
Question 2. How many whole units are there in $\frac{4}{3}$ and in $\frac{7}{3}$?
Answer:
To find the number of whole units in an improper fraction, we can convert it into a mixed number or perform division. The whole number part of the mixed number or the quotient from the division is the number of whole units.
For the fraction $\frac{4}{3}$:
We can divide 4 by 3.
$4 \div 3$
The quotient is 1 and the remainder is 1.
So, we can write $\frac{4}{3}$ as a mixed number:
$\frac{4}{3} = 1 \frac{1}{3}$
This means that $\frac{4}{3}$ is equal to 1 whole unit plus $\frac{1}{3}$ of another unit.
Therefore, there is 1 whole unit in $\frac{4}{3}$.
For the fraction $\frac{7}{3}$:
We can divide 7 by 3.
$7 \div 3$
The quotient is 2 and the remainder is 1.
So, we can write $\frac{7}{3}$ as a mixed number:
$\frac{7}{3} = 2 \frac{1}{3}$
This means that $\frac{7}{3}$ is equal to 2 whole units plus $\frac{1}{3}$ of another unit.
Therefore, there are 2 whole units in $\frac{7}{3}$.
In conclusion, there is 1 whole unit in $\frac{4}{3}$ and there are 2 whole units in $\frac{7}{3}$.
Figure it Out (Page 162 - 163)
Question 1. Figure out the number of whole units in each of the following fractions:
a. $\frac{8}{3}$
b. $\frac{11}{5}$
c. $\frac{9}{4}$
Answer:
To find the number of whole units in an improper fraction, we convert the fraction into a mixed number. The whole number part of the mixed number gives us the number of whole units.
a. For the fraction $\frac{8}{3}$:
We divide 8 by 3.
$8 \div 3 = 2$ with a remainder of 2.
So, the mixed number is $2\frac{2}{3}$.
$\frac{8}{3} = 2 + \frac{2}{3}$
The whole number part is 2.
Therefore, there are 2 whole units in $\frac{8}{3}$.
b. For the fraction $\frac{11}{5}$:
We divide 11 by 5.
$11 \div 5 = 2$ with a remainder of 1.
So, the mixed number is $2\frac{1}{5}$.
$\frac{11}{5} = 2 + \frac{1}{5}$
The whole number part is 2.
Therefore, there are 2 whole units in $\frac{11}{5}$.
c. For the fraction $\frac{9}{4}$:
We divide 9 by 4.
$9 \div 4 = 2$ with a remainder of 1.
So, the mixed number is $2\frac{1}{4}$.
$\frac{9}{4} = 2 + \frac{1}{4}$
The whole number part is 2.
Therefore, there are 2 whole units in $\frac{9}{4}$.
Summary of whole units:
a. In $\frac{8}{3}$, there are 2 whole units.
b. In $\frac{11}{5}$, there are 2 whole units.
c. In $\frac{9}{4}$, there are 2 whole units.
Question 2.
Can all fractions greater than 1 be written as such mixed numbers?
A mixed number / mixed fraction contains a whole number (called the whole part) and a fraction that is less than 1 (called the fractional part).
Answer:
Yes, all fractions greater than 1 can be written as mixed numbers.
A fraction greater than 1 is called an improper fraction, where the numerator is greater than or equal to the denominator. When the numerator is greater than the denominator, the fraction represents one or more whole units plus a part of a unit.
We can convert any improper fraction into a mixed number by dividing the numerator by the denominator. The quotient of this division becomes the whole number part of the mixed number, and the remainder becomes the numerator of the fractional part, with the original denominator remaining the same.
Since the numerator (the original numerator) is greater than the denominator, the quotient will always be at least 1 (representing the whole unit(s)), and the remainder will always be less than the denominator (meaning the fractional part will be less than 1).
For example, for the fraction $\frac{4}{3}$ (which is greater than 1), dividing 4 by 3 gives a quotient of 1 and a remainder of 1. So, $\frac{4}{3}$ can be written as the mixed number $1\frac{1}{3}$. Here, 1 is the whole number part and $\frac{1}{3}$ is the fractional part (which is less than 1).
Therefore, any fraction greater than 1 can be expressed as a combination of a whole number and a proper fraction (a fraction less than 1), which is the definition of a mixed number.
So, the answer is Yes.
Question 3. Write the following fractions as mixed fractions $(e.g., \frac{9}{2} = 4\frac{1}{2})$:
a. $\frac{9}{2}$
b. $\frac{9}{5}$
c. $\frac{21}{19}$
d. $\frac{47}{9}$
e. $\frac{12}{11}$
f. $\frac{19}{6}$
Answer:
To write an improper fraction as a mixed fraction, we divide the numerator by the denominator. The quotient is the whole number part, the remainder is the numerator of the fractional part, and the denominator remains the same.
a. For $\frac{9}{2}$:
Divide 9 by 2.
$9 \div 2 = 4$ with a remainder of 1.
So, the mixed fraction is $4\frac{1}{2}$.
b. For $\frac{9}{5}$:
Divide 9 by 5.
$9 \div 5 = 1$ with a remainder of 4.
So, the mixed fraction is $1\frac{4}{5}$.
c. For $\frac{21}{19}$:
Divide 21 by 19.
$21 \div 19 = 1$ with a remainder of 2.
So, the mixed fraction is $1\frac{2}{19}$.
d. For $\frac{47}{9}$:
Divide 47 by 9.
$47 \div 9 = 5$ with a remainder of 2.
So, the mixed fraction is $5\frac{2}{9}$.
e. For $\frac{12}{11}$:
Divide 12 by 11.
$12 \div 11 = 1$ with a remainder of 1.
So, the mixed fraction is $1\frac{1}{11}$.
f. For $\frac{19}{6}$:
Divide 19 by 6.
$19 \div 6 = 3$ with a remainder of 1.
So, the mixed fraction is $3\frac{1}{6}$.
Figure it Out (Page 163)
Write the following mixed numbers as fractions:
a. $3\frac{1}{4}$
b. $7\frac{2}{3}$
c. $9\frac{4}{9}$
d. $3\frac{1}{6}$
e. $2\frac{3}{11}$
f. $3\frac{9}{10}$
Answer:
To convert a mixed number to an improper fraction, we multiply the whole number by the denominator of the fraction, add the numerator, and place the result over the original denominator.
The formula is: $\text{Mixed Number} = \text{Whole Number} \frac{\text{Numerator}}{\text{Denominator}} \implies \text{Improper Fraction} = \frac{(\text{Whole Number} \times \text{Denominator}) + \text{Numerator}}{\text{Denominator}}$.
a. For $3\frac{1}{4}$:
Whole number = 3, Numerator = 1, Denominator = 4.
Numerator of improper fraction = $(3 \times 4) + 1 = 12 + 1 = 13$.
The denominator remains 4.
So, $3\frac{1}{4} = \textbf{\frac{13}{4}}$.
b. For $7\frac{2}{3}$:
Whole number = 7, Numerator = 2, Denominator = 3.
Numerator of improper fraction = $(7 \times 3) + 2 = 21 + 2 = 23$.
The denominator remains 3.
So, $7\frac{2}{3} = \textbf{\frac{23}{3}}$.
c. For $9\frac{4}{9}$:
Whole number = 9, Numerator = 4, Denominator = 9.
Numerator of improper fraction = $(9 \times 9) + 4 = 81 + 4 = 85$.
The denominator remains 9.
So, $9\frac{4}{9} = \textbf{\frac{85}{9}}$.
d. For $3\frac{1}{6}$:
Whole number = 3, Numerator = 1, Denominator = 6.
Numerator of improper fraction = $(3 \times 6) + 1 = 18 + 1 = 19$.
The denominator remains 6.
So, $3\frac{1}{6} = \textbf{\frac{19}{6}}$.
e. For $2\frac{3}{11}$:
Whole number = 2, Numerator = 3, Denominator = 11.
Numerator of improper fraction = $(2 \times 11) + 3 = 22 + 3 = 25$.
The denominator remains 11.
So, $2\frac{3}{11} = \textbf{\frac{25}{11}}$.
f. For $3\frac{9}{10}$:
Whole number = 3, Numerator = 9, Denominator = 10.
Numerator of improper fraction = $(3 \times 10) + 9 = 30 + 9 = 39$.
The denominator remains 10.
So, $3\frac{9}{10} = \textbf{\frac{39}{10}}$.
Intext Question (Page 164 - 165)

Question: Answer the following questions after looking at the fraction wall:
1. Are the lengths $\frac{1}{2}$ and $\frac{3}{6}$ equal?
2. Are $\frac{2}{3}$ and $\frac{4}{6}$ equivalent fractions? Why?
3. How many pieces of length $\frac{1}{6}$ will make a length of $\frac{1}{2}$ ?
4. How many pieces of length $\frac{1}{6}$ will make a length of $\frac{1}{3}$ ?
Answer:
Based on the fraction wall:
1. Look at the rows corresponding to $\frac{1}{2}$ and $\frac{1}{6}$. One piece of $\frac{1}{2}$ spans the same length as three pieces of $\frac{1}{6}$ (since $\frac{3}{6}$ simplifies to $\frac{1}{2}$).
So, yes, the lengths $\frac{1}{2}$ and $\frac{3}{6}$ are equal.
2. Look at the row for $\frac{1}{3}$. The length for $\frac{2}{3}$ is obtained by taking two pieces of $\frac{1}{3}$. Look at the row for $\frac{1}{6}$. The length for $\frac{4}{6}$ is obtained by taking four pieces of $\frac{1}{6}$.
Comparing these lengths on the fraction wall, we see that they are the same.
So, yes, $\frac{2}{3}$ and $\frac{4}{6}$ are equivalent fractions.
They are equivalent because $\frac{4}{6}$ can be simplified by dividing the numerator and denominator by their greatest common divisor, 2:
$\frac{4}{6} = \frac{4 \div 2}{6 \div 2} = \frac{2}{3}$
Thus, they represent the same value.
3. To make a length of $\frac{1}{2}$ using pieces of length $\frac{1}{6}$, we look at the fraction wall and see how many $\frac{1}{6}$ segments align with the length of one $\frac{1}{2}$ segment.
From the wall, we can see that 3 pieces of $\frac{1}{6}$ make the same length as 1 piece of $\frac{1}{2}$. This is because $\frac{3}{6} = \frac{1}{2}$.
Therefore, 3 pieces of length $\frac{1}{6}$ will make a length of $\frac{1}{2}$.
4. To make a length of $\frac{1}{3}$ using pieces of length $\frac{1}{6}$, we look at the fraction wall and see how many $\frac{1}{6}$ segments align with the length of one $\frac{1}{3}$ segment.
From the wall, we can see that 2 pieces of $\frac{1}{6}$ make the same length as 1 piece of $\frac{1}{3}$. This is because $\frac{2}{6} = \frac{1}{3}$.
Therefore, 2 pieces of length $\frac{1}{6}$ will make a length of $\frac{1}{3}$.
Figure it Out (Page 165)
Question 1. Are $\frac{3}{6}$, $\frac{4}{8}$, $\frac{5}{10}$ equivalent fractions? Why?
Answer:
Yes, the fractions $\frac{3}{6}$, $\frac{4}{8}$, and $\frac{5}{10}$ are equivalent fractions.
Equivalent fractions are fractions that represent the same value, even though they may look different. We can check if fractions are equivalent by simplifying them to their lowest terms or by cross-multiplication.
Let's simplify each fraction:
For $\frac{3}{6}$:
Divide the numerator and the denominator by their greatest common divisor, which is 3.
$\frac{3 \div 3}{6 \div 3} = \frac{1}{2}$
For $\frac{4}{8}$:
Divide the numerator and the denominator by their greatest common divisor, which is 4.
$\frac{4 \div 4}{8 \div 4} = \frac{1}{2}$
For $\frac{5}{10}$:
Divide the numerator and the denominator by their greatest common divisor, which is 5.
$\frac{5 \div 5}{10 \div 5} = \frac{1}{2}$
Since all three fractions simplify to the same fraction, $\frac{1}{2}$, they represent the same value.
Therefore, $\frac{3}{6}$, $\frac{4}{8}$, and $\frac{5}{10}$ are indeed equivalent fractions.
Question 2. Write two equivalent fractions for $\frac{2}{6}$ .
Answer:
The given fraction is $\frac{2}{6}$.
To find equivalent fractions, we multiply the numerator and the denominator by the same non-zero integer.
Let's multiply the numerator and denominator by 2:
$\frac{2}{6} = \frac{2 \times 2}{6 \times 2} = \frac{4}{12}$
Let's multiply the numerator and denominator by 3:
$\frac{2}{6} = \frac{2 \times 3}{6 \times 3} = \frac{6}{18}$
Therefore, two equivalent fractions for $\frac{2}{6}$ are $\frac{4}{12}$ and $\frac{6}{18}$.
Question 3. $\frac{4}{6}$ = $\frac{-}{-}$ = $\frac{-}{-}$ = $\frac{-}{-}$ = ............ (Write as many as you can)
Answer:
The given fraction is $\frac{4}{6}$.
Equivalent fractions can be found by multiplying or dividing both the numerator and the denominator by the same non-zero integer.
First, let's simplify the fraction by dividing the numerator and denominator by their greatest common divisor, which is 2:
$\frac{4}{6} = \frac{4 \div 2}{6 \div 2} = \frac{2}{3}$
Now, let's find other equivalent fractions by multiplying the numerator and denominator by different integers:
Multiply by 2:
$\frac{4}{6} = \frac{4 \times 2}{6 \times 2} = \frac{8}{12}$
Multiply by 3:
$\frac{4}{6} = \frac{4 \times 3}{6 \times 3} = \frac{12}{18}$
Multiply by 4:
$\frac{4}{6} = \frac{4 \times 4}{6 \times 4} = \frac{16}{24}$
Multiply by 5:
$\frac{4}{6} = \frac{4 \times 5}{6 \times 5} = \frac{20}{30}$
So, we can write:
$\frac{4}{6} = \frac{2}{3} = \frac{8}{12} = \frac{12}{18} = \frac{16}{24} = \frac{20}{30} = \dots$
Figure it Out (Page 166)

Question 1. Three rotis are shared equally by four children. Show the division in the picture and write a fraction for how much each child gets. Also, write the corresponding division facts, addition facts, and, multiplication facts.
Fraction of roti each child gets is ______.
Division fact:
Addition fact:
Multiplication fact:
Compare your picture and answers with your classmates!
Answer:
Given:
Number of rotis = 3
Number of children = 4
To Find:
Fraction of roti each child gets, Division fact, Addition fact, and Multiplication fact.
Solution:
To share the 3 rotis equally among 4 children, we can divide each roti into 4 equal parts.
Each child gets 1 part from each of the 3 rotis.
So, each child gets a total of 3 parts.
Since each roti was divided into 4 parts, each part is $\frac{1}{4}$ of a roti.
Therefore, each child gets 3 parts of $\frac{1}{4}$ each.
Fraction of roti each child gets is the total number of rotis divided by the number of children.
Fraction = $\frac{\text{Number of rotis}}{\text{Number of children}} = \frac{3}{4}$
Fraction of roti each child gets is $\frac{3}{4}$.
Division fact:
When 3 rotis are divided equally among 4 children, each child gets $\frac{3}{4}$ of a roti.
The division fact is $3 \div 4 = \frac{3}{4}$.
Addition fact:
If we sum up the portions received by the four children, the total must be the initial number of rotis (3).
Portion of Child 1 + Portion of Child 2 + Portion of Child 3 + Portion of Child 4 = Total rotis
$\frac{3}{4} + \frac{3}{4} + \frac{3}{4} + \frac{3}{4} = \frac{3+3+3+3}{4} = \frac{12}{4} = 3$
The addition fact is $\frac{3}{4} + \frac{3}{4} + \frac{3}{4} + \frac{3}{4} = 3$.
Multiplication fact:
Since 4 children each receive $\frac{3}{4}$ of a roti, the total amount is the number of children multiplied by the portion each child receives.
Number of children $\times$ Portion per child = Total rotis
$4 \times \frac{3}{4} = \frac{4 \times 3}{4} = \frac{12}{4} = 3$
The multiplication fact is $4 \times \frac{3}{4} = 3$.
Question 2. Draw a picture to show how much each child gets when 2 rotis are shared equally by 4 children. Also, write the corresponding division facts, addition facts, and multiplication facts.
Answer:
Given:
Number of rotis = 2
Number of children = 4
To Find:
Fraction of roti each child gets, Picture representation, Division fact, Addition fact, and Multiplication fact.
Solution:
To share 2 rotis equally among 4 children, the fraction of roti each child gets is the total number of rotis divided by the number of children.
Fraction = $\frac{\text{Number of rotis}}{\text{Number of children}} = \frac{2}{4}$
Simplifying the fraction:
$\frac{2}{4} = \frac{\cancel{2}^{1}}{\cancel{4}_{2}} = \frac{1}{2}$
Fraction of roti each child gets is $\frac{1}{2}$.
Picture Representation:
Imagine two circular rotis. To divide them equally among 4 children, each roti can be cut into two equal halves. There will be a total of 4 halves (2 halves from the first roti + 2 halves from the second roti). Each child receives one half from the total of 4 halves.
A picture would show two circles, each divided in half by a line. Each half could be labeled as $\frac{1}{2}$. Arrows could point from one half of the first roti and one half of the second roti to represent the total amount ($\frac{1}{2} + \frac{1}{2} = 1$ whole roti equivalent per two children, or $\frac{1}{2}$ per child).
Division fact:
When 2 rotis are divided equally among 4 children, each child gets $\frac{1}{2}$ of a roti.
The division fact is $2 \div 4 = \frac{1}{2}$.
Addition fact:
The sum of the portions received by the four children equals the total number of rotis.
$\frac{1}{2} + \frac{1}{2} + \frac{1}{2} + \frac{1}{2} = \frac{1+1+1+1}{2} = \frac{4}{2} = 2$
The addition fact is $\frac{1}{2} + \frac{1}{2} + \frac{1}{2} + \frac{1}{2} = 2$.
Multiplication fact:
The number of children multiplied by the portion each child receives equals the total number of rotis.
$4 \times \frac{1}{2} = \frac{4 \times 1}{2} = \frac{4}{2} = 2$
The multiplication fact is $4 \times \frac{1}{2} = 2$.
Question 3. Anil was in a group where 2 cakes were divided equally among 5 children. How much cake would Anil get?
Answer:
Given:
Number of cakes = 2
Number of children = 5
To Find:
Amount of cake Anil gets.
Solution:
When 2 cakes are divided equally among 5 children, each child gets the total number of cakes divided by the number of children.
Amount each child gets = $\frac{\text{Number of cakes}}{\text{Number of children}} = \frac{2}{5}$
Since Anil is one of the 5 children and the cakes are divided equally, the amount of cake Anil gets is the same as what any other child gets.
The amount of cake Anil gets is $\frac{2}{5}$ of a cake.
Figure it Out (Page 168 - 169)
Find the missing numbers:
a. 5 glasses of juice shared equally among 4 friends is the same as ____ glasses of juice shared equally among 8 friends. So, $\frac{5}{4}$ = $\frac{-}{8}$ .
b. 4 kg of potatoes divided equally in 3 bags is the same as 12 kgs of potatoes divided equally in ___ bags. So, $\frac{4}{3}$ = $\frac{12}{-}$
c. 7 rotis divided among 5 children is the same as____rotis divided among _____ children. So, $\frac{7}{5}$ = $\frac{-}{-}$ .
Answer:
To find the missing numbers in equivalent fractions, we need to identify the factor by which the numerator or denominator has been multiplied or divided, and apply the same factor to the other part of the fraction.
a. We are given the relationship: $\frac{5}{4} = \frac{?}{8}$.
We observe the change in the denominator from 4 to 8. To get 8 from 4, we multiply by 2 ($4 \times 2 = 8$).
To keep the fraction equivalent, we must multiply the numerator by the same factor:
$5 \times 2 = 10$.
So, the missing number is 10.
5 glasses of juice shared equally among 4 friends is the same as 10 glasses of juice shared equally among 8 friends.
Thus, $\frac{5}{4} = \frac{10}{8}$.
b. We are given the relationship: $\frac{4}{3} = \frac{12}{?}$.
We observe the change in the numerator from 4 to 12. To get 12 from 4, we multiply by 3 ($4 \times 3 = 12$).
To keep the fraction equivalent, we must multiply the denominator by the same factor:
$3 \times 3 = 9$.
So, the missing number is 9.
4 kg of potatoes divided equally in 3 bags is the same as 12 kgs of potatoes divided equally in 9 bags.
Thus, $\frac{4}{3} = \frac{12}{9}$.
c. We are given the relationship: $\frac{7}{5} = \frac{?}{?}$.
We need to find an equivalent fraction for $\frac{7}{5}$. We can multiply both the numerator and the denominator by any non-zero integer. Let's multiply by 2.
Numerator: $7 \times 2 = 14$.
Denominator: $5 \times 2 = 10$.
So, one possible equivalent fraction is $\frac{14}{10}$.
7 rotis divided among 5 children is the same as 14 rotis divided among 10 children.
Thus, $\frac{7}{5} = \frac{14}{10}$. (Other equivalent fractions are also possible, for example, multiplying by 3 gives $\frac{21}{15}$).
Intext Question (Page 169)
Question: In which group will each child get more chikki?
1 chikki divided between 2 children or 5 chikkis divided among 8 children.
Answer:
Given:
Scenario 1: 1 chikki divided between 2 children.
Scenario 2: 5 chikkis divided among 8 children.
To Find:
In which scenario each child gets more chikki.
Solution:
In the first scenario, 1 chikki is divided between 2 children. The fraction of chikki each child gets is $\frac{1}{2}$.
In the second scenario, 5 chikkis are divided among 8 children. The fraction of chikki each child gets is $\frac{5}{8}$.
To compare which fraction is larger, we need to compare $\frac{1}{2}$ and $\frac{5}{8}$.
We can compare these fractions by finding a common denominator. The least common multiple (LCM) of the denominators 2 and 8 is 8.
Convert $\frac{1}{2}$ to an equivalent fraction with a denominator of 8:
$\frac{1}{2} = \frac{1 \times 4}{2 \times 4} = \frac{4}{8}$
Now compare the fractions $\frac{4}{8}$ and $\frac{5}{8}$.
Since the denominators are the same, we compare the numerators.
Comparing the numerators 4 and 5, we see that $5 > 4$.
Therefore, $\frac{5}{8} > \frac{4}{8}$.
This means $\frac{5}{8}$ is greater than $\frac{1}{2}$.
So, each child gets more chikki in the group where 5 chikkis are divided among 8 children.
Answer: Each child will get more chikki in the group where 5 chikkis are divided among 8 children.
Intext Question (Page 169)
Question: What about the following groups? In which group will each child get more?
1 chikki divided between 2 children or 4 chikkis divided among 7 children.
Answer:
Given:
Scenario 1: 1 chikki divided between 2 children.
Scenario 2: 4 chikkis divided among 7 children.
To Find:
In which scenario each child gets more chikki.
Solution:
In the first scenario, 1 chikki is divided between 2 children. The fraction of chikki each child gets is $\frac{1}{2}$.
In the second scenario, 4 chikkis are divided among 7 children. The fraction of chikki each child gets is $\frac{4}{7}$.
To compare which fraction is larger, we need to compare $\frac{1}{2}$ and $\frac{4}{7}$.
We can compare these fractions by finding a common denominator. The least common multiple (LCM) of the denominators 2 and 7 is 14.
Convert $\frac{1}{2}$ to an equivalent fraction with a denominator of 14:
$\frac{1}{2} = \frac{1 \times 7}{2 \times 7} = \frac{7}{14}$
Convert $\frac{4}{7}$ to an equivalent fraction with a denominator of 14:
$\frac{4}{7} = \frac{4 \times 2}{7 \times 2} = \frac{8}{14}$
Now compare the fractions $\frac{7}{14}$ and $\frac{8}{14}$.
Since the denominators are the same, we compare the numerators.
Comparing the numerators 7 and 8, we see that $8 > 7$.
Therefore, $\frac{8}{14} > \frac{7}{14}$.
This means $\frac{4}{7} > \frac{1}{2}$.
So, each child gets more chikki in the group where 4 chikkis are divided among 7 children.
Answer: Each child will get more chikki in the group where 4 chikkis are divided among 7 children.
Intext Question (Page 170)
Question: Suppose the number of children is kept the same, but the number of units that are being shared is increased? What can you say about each child’s share now? Why? Discuss how your reasoning explains
$\frac{1}{5}$ < $\frac{2}{5}$ , $\frac{3}{7}$ < $\frac{4}{7}$ , and $\frac{1}{2}$ < $\frac{5}{8}$ .
Answer:
Given:
The number of children is kept the same.
The number of units (items) being shared is increased.
Discussion and Reasoning:
When a certain number of items are shared equally among a fixed number of people, the fraction representing each person's share is given by $\frac{\text{Number of items}}{\text{Number of people}}$.
If the number of people (the denominator of the fraction) remains constant, and the number of items (the numerator of the fraction) increases, each person will receive a larger portion.
This is because there are more items to distribute among the same number of people, so each person's share of the total increases proportionally to the increase in the number of items.
We can say that if the number of children is kept the same, but the number of units that are being shared is increased, then each child's share will increase.
The reason is that with a fixed denominator (number of children), a larger numerator (number of units) means a larger value for the fraction, which represents a larger share for each individual.
Let's see how this reasoning explains the given inequalities:
1. $\frac{1}{5} < \frac{2}{5}$:
Here, the denominator is 5 (number of children). The numerator increases from 1 to 2 (number of units increases).
Sharing 1 unit among 5 children gives each child $\frac{1}{5}$. Sharing 2 units among 5 children gives each child $\frac{2}{5}$.
Since $2 > 1$, and the number of children is the same (5), each child gets more when 2 units are shared than when 1 unit is shared. Thus, $\frac{1}{5} < \frac{2}{5}$.
2. $\frac{3}{7} < \frac{4}{7}$:
Here, the denominator is 7 (number of children). The numerator increases from 3 to 4 (number of units increases).
Sharing 3 units among 7 children gives each child $\frac{3}{7}$. Sharing 4 units among 7 children gives each child $\frac{4}{7}$.
Since $4 > 3$, and the number of children is the same (7), each child gets more when 4 units are shared than when 3 units are shared. Thus, $\frac{3}{7} < \frac{4}{7}$.
3. $\frac{1}{2} < \frac{5}{8}$:
This inequality compares fractions with different denominators, so the direct reasoning about increasing the numerator with a fixed denominator doesn't apply as directly as in the first two cases.
To compare these, we find a common denominator, which is 8.
$\frac{1}{2} = \frac{1 \times 4}{2 \times 4} = \frac{4}{8}$
Now we compare $\frac{4}{8}$ and $\frac{5}{8}$.
This can be interpreted as sharing 4 units among 8 children versus sharing 5 units among 8 children. The number of children is fixed at 8, and the number of units increases from 4 to 5.
Following the same reasoning as above, when the number of units increases from 4 to 5 while the number of sharers remains 8, the share per person increases.
Since $5 > 4$, and the number of children is the same (8), each child gets more when 5 units are shared than when 4 units are shared.
Thus, $\frac{4}{8} < \frac{5}{8}$, which means $\frac{1}{2} < \frac{5}{8}$.
In summary, for fractions with the same denominator, the fraction with the larger numerator is the larger fraction. This corresponds to a scenario where the number of items increases while the number of sharers stays the same, resulting in a larger share per sharer.
Intext Question (Page 170)
Question: Now, decide in which of the two groups will each child get a larger share:
1. Group 1: 3 glasses of sugarcane juice divided equally among 4 children.
Group 2: 7 glasses of sugarcane juice divided equally among 10 children.
2. Group 1: 4 glasses of sugarcane juice divided equally among 7 children.
Group 2: 5 glasses of sugarcane juice divided equally among 7 children.
Answer:
To determine which group gives each child a larger share, we need to express the share each child receives as a fraction and then compare the fractions.
For Question 1:
In Group 1, 3 glasses of juice are divided among 4 children. The share for each child is $\frac{3}{4}$ of a glass.
In Group 2, 7 glasses of juice are divided among 10 children. The share for each child is $\frac{7}{10}$ of a glass.
We need to compare $\frac{3}{4}$ and $\frac{7}{10}$.
To compare fractions with different denominators, we can find a common denominator. The least common multiple (LCM) of 4 and 10 is 20.
Convert $\frac{3}{4}$ to an equivalent fraction with a denominator of 20:
$\frac{3}{4} = \frac{3 \times 5}{4 \times 5} = \frac{15}{20}$
Convert $\frac{7}{10}$ to an equivalent fraction with a denominator of 20:
$\frac{7}{10} = \frac{7 \times 2}{10 \times 2} = \frac{14}{20}$
Now we compare $\frac{15}{20}$ and $\frac{14}{20}$. Since the denominators are the same, we compare the numerators.
$15 > 14$, so $\frac{15}{20} > \frac{14}{20}$.
This means $\frac{3}{4} > \frac{7}{10}$.
Therefore, each child gets a larger share in Group 1.
For Question 2:
In Group 1, 4 glasses of juice are divided among 7 children. The share for each child is $\frac{4}{7}$ of a glass.
In Group 2, 5 glasses of juice are divided among 7 children. The share for each child is $\frac{5}{7}$ of a glass.
We need to compare $\frac{4}{7}$ and $\frac{5}{7}$.
Since the denominators are the same (7), we can directly compare the numerators.
$4 < 5$, so $\frac{4}{7} < \frac{5}{7}$.
Therefore, each child gets a larger share in Group 2.
Intext Question (Page 172)
Question: Find equivalent fractions for the given pairs of fractions such that the fractional units are the same.
a. $\frac{7}{2}$ and $\frac{3}{5}$
b. $\frac{8}{3}$ and $\frac{5}{6}$
c. $\frac{3}{4}$ and $\frac{3}{5}$
d. $\frac{6}{7}$ and $\frac{8}{5}$
e. $\frac{9}{4}$ and $\frac{5}{2}$
f. $\frac{1}{10}$ and $\frac{2}{9}$
g. $\frac{8}{3}$ and $\frac{11}{4}$
h. $\frac{13}{6}$ and $\frac{1}{9}$
Answer:
To find equivalent fractions with the same fractional unit, we need to rewrite the fractions with a common denominator. The least common denominator (LCD) is the least common multiple (LCM) of the denominators.
a. Given fractions are $\frac{7}{2}$ and $\frac{3}{5}$.
Denominators are 2 and 5.
LCM(2, 5) = 10.
Convert $\frac{7}{2}$ to an equivalent fraction with denominator 10:
$\frac{7}{2} = \frac{7 \times 5}{2 \times 5} = \frac{35}{10}$
Convert $\frac{3}{5}$ to an equivalent fraction with denominator 10:
$\frac{3}{5} = \frac{3 \times 2}{5 \times 2} = \frac{6}{10}$
The equivalent fractions with the same fractional unit are $\frac{35}{10}$ and $\frac{6}{10}$.
b. Given fractions are $\frac{8}{3}$ and $\frac{5}{6}$.
Denominators are 3 and 6.
LCM(3, 6) = 6.
Convert $\frac{8}{3}$ to an equivalent fraction with denominator 6:
$\frac{8}{3} = \frac{8 \times 2}{3 \times 2} = \frac{16}{6}$
The fraction $\frac{5}{6}$ already has the denominator 6.
The equivalent fractions with the same fractional unit are $\frac{16}{6}$ and $\frac{5}{6}$.
c. Given fractions are $\frac{3}{4}$ and $\frac{3}{5}$.
Denominators are 4 and 5.
LCM(4, 5) = 20.
Convert $\frac{3}{4}$ to an equivalent fraction with denominator 20:
$\frac{3}{4} = \frac{3 \times 5}{4 \times 5} = \frac{15}{20}$
Convert $\frac{3}{5}$ to an equivalent fraction with denominator 20:
$\frac{3}{5} = \frac{3 \times 4}{5 \times 4} = \frac{12}{20}$
The equivalent fractions with the same fractional unit are $\frac{15}{20}$ and $\frac{12}{20}$.
d. Given fractions are $\frac{6}{7}$ and $\frac{8}{5}$.
Denominators are 7 and 5.
LCM(7, 5) = 35.
Convert $\frac{6}{7}$ to an equivalent fraction with denominator 35:
$\frac{6}{7} = \frac{6 \times 5}{7 \times 5} = \frac{30}{35}$
Convert $\frac{8}{5}$ to an equivalent fraction with denominator 35:
$\frac{8}{5} = \frac{8 \times 7}{5 \times 7} = \frac{56}{35}$
The equivalent fractions with the same fractional unit are $\frac{30}{35}$ and $\frac{56}{35}$.
e. Given fractions are $\frac{9}{4}$ and $\frac{5}{2}$.
Denominators are 4 and 2.
LCM(4, 2) = 4.
The fraction $\frac{9}{4}$ already has the denominator 4.
Convert $\frac{5}{2}$ to an equivalent fraction with denominator 4:
$\frac{5}{2} = \frac{5 \times 2}{2 \times 2} = \frac{10}{4}$
The equivalent fractions with the same fractional unit are $\frac{9}{4}$ and $\frac{10}{4}$.
f. Given fractions are $\frac{1}{10}$ and $\frac{2}{9}$.
Denominators are 10 and 9.
LCM(10, 9) = 90.
Convert $\frac{1}{10}$ to an equivalent fraction with denominator 90:
$\frac{1}{10} = \frac{1 \times 9}{10 \times 9} = \frac{9}{90}$
Convert $\frac{2}{9}$ to an equivalent fraction with denominator 90:
$\frac{2}{9} = \frac{2 \times 10}{9 \times 10} = \frac{20}{90}$
The equivalent fractions with the same fractional unit are $\frac{9}{90}$ and $\frac{20}{90}$.
g. Given fractions are $\frac{8}{3}$ and $\frac{11}{4}$.
Denominators are 3 and 4.
LCM(3, 4) = 12.
Convert $\frac{8}{3}$ to an equivalent fraction with denominator 12:
$\frac{8}{3} = \frac{8 \times 4}{3 \times 4} = \frac{32}{12}$
Convert $\frac{11}{4}$ to an equivalent fraction with denominator 12:
$\frac{11}{4} = \frac{11 \times 3}{4 \times 3} = \frac{33}{12}$
The equivalent fractions with the same fractional unit are $\frac{32}{12}$ and $\frac{33}{12}$.
h. Given fractions are $\frac{13}{6}$ and $\frac{1}{9}$.
Denominators are 6 and 9.
LCM(6, 9) = 18.
Convert $\frac{13}{6}$ to an equivalent fraction with denominator 18:
$\frac{13}{6} = \frac{13 \times 3}{6 \times 3} = \frac{39}{18}$
Convert $\frac{1}{9}$ to an equivalent fraction with denominator 18:
$\frac{1}{9} = \frac{1 \times 2}{9 \times 2} = \frac{2}{18}$
The equivalent fractions with the same fractional unit are $\frac{39}{18}$ and $\frac{2}{18}$.
Figure it Out (Page 173)
Express the following fractions in lowest terms:
a. $\frac{17}{51}$
b. $\frac{64}{144}$
c. $\frac{126}{147}$
d. $\frac{525}{112}$
Answer:
To express a fraction in its lowest terms, we divide both the numerator and the denominator by their greatest common divisor (GCD).
a. Given fraction is $\frac{17}{51}$.
We find the GCD of the numerator 17 and the denominator 51.
17 is a prime number.
We check if 51 is divisible by 17: $51 = 17 \times 3$.
So, the GCD(17, 51) = 17.
Divide the numerator and denominator by 17:
$\frac{17 \div 17}{51 \div 17} = \frac{1}{3}$
The lowest term of $\frac{17}{51}$ is $\frac{1}{3}$.
b. Given fraction is $\frac{64}{144}$.
We find the GCD of 64 and 144.
Using prime factorization:
$64 = 2 \times 2 \times 2 \times 2 \times 2 \times 2 = 2^6$
$144 = 2 \times 72 = 2 \times 2 \times 36 = 2 \times 2 \times 2 \times 18 = 2 \times 2 \times 2 \times 2 \times 9 = 2^4 \times 3^2$
GCD(64, 144) = $2^4 = 16$.
Divide the numerator and denominator by 16:
$\frac{64 \div 16}{144 \div 16} = \frac{4}{9}$
The lowest term of $\frac{64}{144}$ is $\frac{4}{9}$.
c. Given fraction is $\frac{126}{147}$.
We find the GCD of 126 and 147.
Using prime factorization:
$126 = 2 \times 63 = 2 \times 3 \times 21 = 2 \times 3 \times 3 \times 7 = 2 \times 3^2 \times 7$
$147 = 3 \times 49 = 3 \times 7 \times 7 = 3 \times 7^2$
GCD(126, 147) = $3 \times 7 = 21$.
Divide the numerator and denominator by 21:
$\frac{126 \div 21}{147 \div 21} = \frac{6}{7}$
The lowest term of $\frac{126}{147}$ is $\frac{6}{7}$.
d. Given fraction is $\frac{525}{112}$.
We find the GCD of 525 and 112.
Using prime factorization:
$525 = 5 \times 105 = 5 \times 5 \times 21 = 3 \times 5^2 \times 7$
$112 = 2 \times 56 = 2 \times 2 \times 28 = 2 \times 2 \times 2 \times 14 = 2 \times 2 \times 2 \times 2 \times 7 = 2^4 \times 7$
GCD(525, 112) = $7$.
Divide the numerator and denominator by 7:
$\frac{525 \div 7}{112 \div 7} = \frac{75}{16}$
The lowest term of $\frac{525}{112}$ is $\frac{75}{16}$.
Figure it Out (Page 174)
Question 1. Compare the following fractions and justify your answers:
a. $\frac{8}{3}$ , $\frac{5}{2}$
b. $\frac{4}{9}$ , $\frac{3}{7}$
c. $\frac{7}{10}$ , $\frac{9}{14}$
d. $\frac{12}{5}$ , $\frac{8}{5}$
e. $\frac{9}{4}$ , $\frac{5}{2}$
Answer:
To compare fractions, we can find a common denominator and then compare the numerators, or if the denominators are already the same, we just compare the numerators directly.
a. Compare $\frac{8}{3}$ and $\frac{5}{2}$.
The denominators are 3 and 2. The least common multiple (LCM) of 3 and 2 is 6.
Convert $\frac{8}{3}$ to an equivalent fraction with denominator 6:
$\frac{8}{3} = \frac{8 \times 2}{3 \times 2} = \frac{16}{6}$
Convert $\frac{5}{2}$ to an equivalent fraction with denominator 6:
$\frac{5}{2} = \frac{5 \times 3}{2 \times 3} = \frac{15}{6}$
Now compare $\frac{16}{6}$ and $\frac{15}{6}$. Since the denominators are the same, we compare the numerators. $16 > 15$.
Therefore, $\frac{16}{6} > \frac{15}{6}$, which means $\frac{8}{3} > \frac{5}{2}$.
Justification: We converted both fractions to equivalent fractions with a common denominator (6) and compared their numerators. $16 > 15$, so $\frac{8}{3}$ is greater than $\frac{5}{2}$.
b. Compare $\frac{4}{9}$ and $\frac{3}{7}$.
The denominators are 9 and 7. The LCM of 9 and 7 is 63.
Convert $\frac{4}{9}$ to an equivalent fraction with denominator 63:
$\frac{4}{9} = \frac{4 \times 7}{9 \times 7} = \frac{28}{63}$
Convert $\frac{3}{7}$ to an equivalent fraction with denominator 63:
$\frac{3}{7} = \frac{3 \times 9}{7 \times 9} = \frac{27}{63}$
Now compare $\frac{28}{63}$ and $\frac{27}{63}$. Since the denominators are the same, we compare the numerators. $28 > 27$.
Therefore, $\frac{28}{63} > \frac{27}{63}$, which means $\frac{4}{9} > \frac{3}{7}$.
Justification: We converted both fractions to equivalent fractions with a common denominator (63) and compared their numerators. $28 > 27$, so $\frac{4}{9}$ is greater than $\frac{3}{7}$.
c. Compare $\frac{7}{10}$ and $\frac{9}{14}$.
The denominators are 10 and 14. The LCM of 10 and 14 is 70.
Convert $\frac{7}{10}$ to an equivalent fraction with denominator 70:
$\frac{7}{10} = \frac{7 \times 7}{10 \times 7} = \frac{49}{70}$
Convert $\frac{9}{14}$ to an equivalent fraction with denominator 70:
$\frac{9}{14} = \frac{9 \times 5}{14 \times 5} = \frac{45}{70}$
Now compare $\frac{49}{70}$ and $\frac{45}{70}$. Since the denominators are the same, we compare the numerators. $49 > 45$.
Therefore, $\frac{49}{70} > \frac{45}{70}$, which means $\frac{7}{10} > \frac{9}{14}$.
Justification: We converted both fractions to equivalent fractions with a common denominator (70) and compared their numerators. $49 > 45$, so $\frac{7}{10}$ is greater than $\frac{9}{14}$.
d. Compare $\frac{12}{5}$ and $\frac{8}{5}$.
The denominators are 5 and 5. They are the same.
Compare the numerators: 12 and 8. $12 > 8$.
Therefore, $\frac{12}{5} > \frac{8}{5}$.
Justification: Since the fractions have the same denominator, the fraction with the larger numerator is greater. $12 > 8$, so $\frac{12}{5}$ is greater than $\frac{8}{5}$.
e. Compare $\frac{9}{4}$ and $\frac{5}{2}$.
The denominators are 4 and 2. The LCM of 4 and 2 is 4.
The fraction $\frac{9}{4}$ already has the denominator 4.
Convert $\frac{5}{2}$ to an equivalent fraction with denominator 4:
$\frac{5}{2} = \frac{5 \times 2}{2 \times 2} = \frac{10}{4}$
Now compare $\frac{9}{4}$ and $\frac{10}{4}$. Since the denominators are the same, we compare the numerators. $9 < 10$.
Therefore, $\frac{9}{4} < \frac{10}{4}$, which means $\frac{9}{4} < \frac{5}{2}$.
Justification: We converted $\frac{5}{2}$ to an equivalent fraction with a common denominator (4) and compared the numerators. $9 < 10$, so $\frac{9}{4}$ is less than $\frac{5}{2}$.
Question 2. Write the following fractions in ascending order.
a. $\frac{7}{10}$ , $\frac{11}{15}$ , $\frac{2}{5}$
b. $\frac{19}{24}$ , $\frac{5}{6}$ , $\frac{7}{12}$
Answer:
To write fractions in ascending order, we first find a common denominator for all the fractions and then compare their numerators.
a. Given fractions are $\frac{7}{10}$, $\frac{11}{15}$, and $\frac{2}{5}$.
The denominators are 10, 15, and 5.
The least common multiple (LCM) of 10, 15, and 5 is 30.
Convert each fraction to an equivalent fraction with denominator 30:
For $\frac{7}{10}$: $\frac{7}{10} = \frac{7 \times 3}{10 \times 3} = \frac{21}{30}$
For $\frac{11}{15}$: $\frac{11}{15} = \frac{11 \times 2}{15 \times 2} = \frac{22}{30}$
For $\frac{2}{5}$: $\frac{2}{5} = \frac{2 \times 6}{5 \times 6} = \frac{12}{30}$
Now we compare the numerators of the equivalent fractions: 21, 22, and 12.
Arranging the numerators in ascending order: $12 < 21 < 22$.
This corresponds to the fractions: $\frac{12}{30} < \frac{21}{30} < \frac{22}{30}$.
Replacing with the original fractions:
$\frac{2}{5} < \frac{7}{10} < \frac{11}{15}$.
The fractions in ascending order are $\frac{2}{5}$, $\frac{7}{10}$, $\frac{11}{15}$.
b. Given fractions are $\frac{19}{24}$, $\frac{5}{6}$, and $\frac{7}{12}$.
The denominators are 24, 6, and 12.
The least common multiple (LCM) of 24, 6, and 12 is 24.
Convert each fraction to an equivalent fraction with denominator 24:
The fraction $\frac{19}{24}$ already has the denominator 24.
For $\frac{5}{6}$: $\frac{5}{6} = \frac{5 \times 4}{6 \times 4} = \frac{20}{24}$
For $\frac{7}{12}$: $\frac{7}{12} = \frac{7 \times 2}{12 \times 2} = \frac{14}{24}$
Now we compare the numerators of the equivalent fractions: 19, 20, and 14.
Arranging the numerators in ascending order: $14 < 19 < 20$.
This corresponds to the fractions: $\frac{14}{24} < \frac{19}{24} < \frac{20}{24}$.
Replacing with the original fractions:
$\frac{7}{12} < \frac{19}{24} < \frac{5}{6}$.
The fractions in ascending order are $\frac{7}{12}$, $\frac{19}{24}$, $\frac{5}{6}$.
Question 3. Write the following fractions in descending order.
a. $\frac{25}{16}$ , $\frac{7}{8}$ , $\frac{13}{4}$ , $\frac{17}{32}$
b. $\frac{3}{4}$ , $\frac{12}{5}$ , $\frac{7}{12}$ , $\frac{5}{4}$
Answer:
To write fractions in descending order, we need to find a common denominator for all the fractions and then compare their numerators.
a. Given fractions are $\frac{25}{16}$, $\frac{7}{8}$, $\frac{13}{4}$, and $\frac{17}{32}$.
The denominators are 16, 8, 4, and 32.
The least common multiple (LCM) of 16, 8, 4, and 32 is 32.
Convert each fraction to an equivalent fraction with a denominator of 32:
For $\frac{25}{16}$: $\frac{25}{16} = \frac{25 \times 2}{16 \times 2} = \frac{50}{32}$
For $\frac{7}{8}$: $\frac{7}{8} = \frac{7 \times 4}{8 \times 4} = \frac{28}{32}$
For $\frac{13}{4}$: $\frac{13}{4} = \frac{13 \times 8}{4 \times 8} = \frac{104}{32}$
For $\frac{17}{32}$: This fraction already has the denominator 32.
The equivalent fractions are $\frac{50}{32}$, $\frac{28}{32}$, $\frac{104}{32}$, and $\frac{17}{32}$.
Now we compare the numerators: 50, 28, 104, and 17.
Arranging the numerators in descending order: $104 > 50 > 28 > 17$.
This corresponds to the fractions in descending order:
$\frac{104}{32} > \frac{50}{32} > \frac{28}{32} > \frac{17}{32}$
Replacing with the original fractions:
$\frac{13}{4} > \frac{25}{16} > \frac{7}{8} > \frac{17}{32}$.
The fractions in descending order are $\frac{13}{4}$, $\frac{25}{16}$, $\frac{7}{8}$, $\frac{17}{32}$.
b. Given fractions are $\frac{3}{4}$, $\frac{12}{5}$, $\frac{7}{12}$, and $\frac{5}{4}$.
The denominators are 4, 5, 12, and 4. The unique denominators are 4, 5, and 12.
The least common multiple (LCM) of 4, 5, and 12 is 60.
$\begin{array}{c|cc} 2 & 4 \;, & 5 \;, & 12 \\ \hline 2 & 2 \; , & 5 \; , & 6 \\ \hline 3 & 1 \; , & 5 \; , & 3 \\ \hline 5 & 1 \; , & 1 \; , & 1 \\ \hline & 1 \; , & 1 \; , & 1 \end{array}$
LCM = $2 \times 2 \times 3 \times 5 = 60$.
Convert each fraction to an equivalent fraction with a denominator of 60:
For $\frac{3}{4}$: $\frac{3}{4} = \frac{3 \times 15}{4 \times 15} = \frac{45}{60}$
For $\frac{12}{5}$: $\frac{12}{5} = \frac{12 \times 12}{5 \times 12} = \frac{144}{60}$
For $\frac{7}{12}$: $\frac{7}{12} = \frac{7 \times 5}{12 \times 5} = \frac{35}{60}$
For $\frac{5}{4}$: $\frac{5}{4} = \frac{5 \times 15}{4 \times 15} = \frac{75}{60}$
The equivalent fractions are $\frac{45}{60}$, $\frac{144}{60}$, $\frac{35}{60}$, and $\frac{75}{60}$.
Now we compare the numerators: 45, 144, 35, and 75.
Arranging the numerators in descending order: $144 > 75 > 45 > 35$.
This corresponds to the fractions in descending order:
$\frac{144}{60} > \frac{75}{60} > \frac{45}{60} > \frac{35}{60}$
Replacing with the original fractions:
$\frac{12}{5} > \frac{5}{4} > \frac{3}{4} > \frac{7}{12}$.
The fractions in descending order are $\frac{12}{5}$, $\frac{5}{4}$, $\frac{3}{4}$, $\frac{7}{12}$.
Intext Question (Page 177)
Question: Try adding $\frac{4}{7}$ + $\frac{6}{7}$ using a number line. Do you get the same answer?
Answer:
Given:
Addition problem: $\frac{4}{7} + \frac{6}{7}$
To Find:
The sum using a number line and compare it with the standard addition method.
Solution using Number Line:
To add fractions with the same denominator on a number line, we first draw a number line and mark points representing fractions with that denominator. In this case, the denominator is 7, so the fractional unit is $\frac{1}{7}$. We mark points like $0, \frac{1}{7}, \frac{2}{7}, \frac{3}{7}, \dots, \frac{7}{7}(=1), \frac{8}{7}, \dots$
Starting from 0, we represent the first fraction $\frac{4}{7}$ by moving 4 units of size $\frac{1}{7}$ to the right.
This takes us to the point $\frac{4}{7}$ on the number line.
From the point $\frac{4}{7}$, we represent the second fraction $\frac{6}{7}$ by moving another 6 units of size $\frac{1}{7}$ to the right (since we are adding).
Starting from $\frac{4}{7}$, moving 1 unit right reaches $\frac{5}{7}$.
Moving 2 units right reaches $\frac{6}{7}$.
Moving 3 units right reaches $\frac{7}{7}$ (or 1).
Moving 4 units right reaches $\frac{8}{7}$.
Moving 5 units right reaches $\frac{9}{7}$.
Moving 6 units right reaches $\frac{10}{7}$.
The final position on the number line is $\frac{10}{7}$.
So, using the number line, $\frac{4}{7} + \frac{6}{7} = \frac{10}{7}$.
Solution using Standard Addition Method:
When adding fractions with the same denominator (like fractions), we add the numerators and keep the denominator the same.
$\frac{4}{7} + \frac{6}{7} = \frac{4+6}{7}$
$\frac{4+6}{7} = \frac{10}{7}$
So, using the standard method, $\frac{4}{7} + \frac{6}{7} = \frac{10}{7}$.
Comparison:
From the number line method, the sum is $\frac{10}{7}$.
From the standard addition method, the sum is $\frac{10}{7}$.
Both methods give the same answer.
Yes, I get the same answer using the number line.
Figure it Out (Page 179)
Question 1. Add the following fractions using Brahmagupta’s method:
a. $\frac{2}{7}$ + $\frac{5}{7}$ + $\frac{6}{7}$
b. $\frac{3}{4}$ + $\frac{1}{3}$
c. $\frac{2}{3}$ + $\frac{5}{6}$
d. $\frac{2}{3}$ + $\frac{2}{7}$
e. $\frac{3}{4}$ + $\frac{1}{3}$ + $\frac{1}{5}$
f. $\frac{2}{3}$ + $\frac{4}{5}$
g. $\frac{4}{5}$ + $\frac{2}{3}$
h. $\frac{3}{5}$ + $\frac{5}{8}$
i. $\frac{9}{2}$ + $\frac{5}{4}$
j. $\frac{8}{3}$ + $\frac{2}{7}$
k. $\frac{3}{4}$ + $\frac{1}{3}$ + $\frac{1}{5}$
l. $\frac{2}{3}$ + $\frac{4}{5}$ + $\frac{3}{7}$
m. $\frac{9}{2}$ + $\frac{5}{4}$ + $\frac{7}{6}$
Answer:
Brahmagupta's method for adding fractions $\frac{a}{b}$ and $\frac{c}{d}$ gives the sum as $\frac{ad + bc}{bd}$. This method relies on finding a common denominator, which is the product of the denominators or their least common multiple (LCM). We will use the general method of finding the LCM of the denominators, which is equivalent to Brahmagupta's principle.
a. Add $\frac{2}{7}$ + $\frac{5}{7}$ + $\frac{6}{7}$.
The fractions have the same denominator (7).
Add the numerators and keep the common denominator:
$\frac{2}{7} + \frac{5}{7} + \frac{6}{7} = \frac{2+5+6}{7} = \frac{13}{7}$
The sum is $\frac{13}{7}$.
b. Add $\frac{3}{4}$ + $\frac{1}{3}$.
The denominators are 4 and 3. The LCM(4, 3) = 12.
Convert fractions to equivalent fractions with denominator 12:
$\frac{3}{4} = \frac{3 \times 3}{4 \times 3} = \frac{9}{12}$
$\frac{1}{3} = \frac{1 \times 4}{3 \times 4} = \frac{4}{12}$
Add the equivalent fractions:
$\frac{9}{12} + \frac{4}{12} = \frac{9+4}{12} = \frac{13}{12}$
The sum is $\frac{13}{12}$.
c. Add $\frac{2}{3}$ + $\frac{5}{6}$.
The denominators are 3 and 6. The LCM(3, 6) = 6.
Convert fractions to equivalent fractions with denominator 6:
$\frac{2}{3} = \frac{2 \times 2}{3 \times 2} = \frac{4}{6}$
The fraction $\frac{5}{6}$ already has the denominator 6.
Add the equivalent fractions:
$\frac{4}{6} + \frac{5}{6} = \frac{4+5}{6} = \frac{9}{6}$
Simplify the result:
$\frac{9}{6} = \frac{\cancel{9}^{3}}{\cancel{6}_{2}} = \frac{3}{2}$
The sum is $\frac{3}{2}$.
d. Add $\frac{2}{3}$ + $\frac{2}{7}$.
The denominators are 3 and 7. The LCM(3, 7) = 21.
Convert fractions to equivalent fractions with denominator 21:
$\frac{2}{3} = \frac{2 \times 7}{3 \times 7} = \frac{14}{21}$
$\frac{2}{7} = \frac{2 \times 3}{7 \times 3} = \frac{6}{21}$
Add the equivalent fractions:
$\frac{14}{21} + \frac{6}{21} = \frac{14+6}{21} = \frac{20}{21}$
The sum is $\frac{20}{21}$.
e. Add $\frac{3}{4}$ + $\frac{1}{3}$ + $\frac{1}{5}$.
The denominators are 4, 3, and 5. The LCM(4, 3, 5) = 60.
Convert fractions to equivalent fractions with denominator 60:
$\frac{3}{4} = \frac{3 \times 15}{4 \times 15} = \frac{45}{60}$
$\frac{1}{3} = \frac{1 \times 20}{3 \times 20} = \frac{20}{60}$
$\frac{1}{5} = \frac{1 \times 12}{5 \times 12} = \frac{12}{60}$
Add the equivalent fractions:
$\frac{45}{60} + \frac{20}{60} + \frac{12}{60} = \frac{45+20+12}{60} = \frac{77}{60}$
The sum is $\frac{77}{60}$.
f. Add $\frac{2}{3}$ + $\frac{4}{5}$.
The denominators are 3 and 5. The LCM(3, 5) = 15.
Convert fractions to equivalent fractions with denominator 15:
$\frac{2}{3} = \frac{2 \times 5}{3 \times 5} = \frac{10}{15}$
$\frac{4}{5} = \frac{4 \times 3}{5 \times 3} = \frac{12}{15}$
Add the equivalent fractions:
$\frac{10}{15} + \frac{12}{15} = \frac{10+12}{15} = \frac{22}{15}$
The sum is $\frac{22}{15}$.
g. Add $\frac{4}{5}$ + $\frac{2}{3}$.
This is the same addition problem as in part f, just with the fractions in a different order. Addition is commutative.
The sum is $\frac{22}{15}$.
h. Add $\frac{3}{5}$ + $\frac{5}{8}$.
The denominators are 5 and 8. The LCM(5, 8) = 40.
Convert fractions to equivalent fractions with denominator 40:
$\frac{3}{5} = \frac{3 \times 8}{5 \times 8} = \frac{24}{40}$
$\frac{5}{8} = \frac{5 \times 5}{8 \times 5} = \frac{25}{40}$
Add the equivalent fractions:
$\frac{24}{40} + \frac{25}{40} = \frac{24+25}{40} = \frac{49}{40}$
The sum is $\frac{49}{40}$.
i. Add $\frac{9}{2}$ + $\frac{5}{4}$.
The denominators are 2 and 4. The LCM(2, 4) = 4.
Convert fractions to equivalent fractions with denominator 4:
$\frac{9}{2} = \frac{9 \times 2}{2 \times 2} = \frac{18}{4}$
The fraction $\frac{5}{4}$ already has the denominator 4.
Add the equivalent fractions:
$\frac{18}{4} + \frac{5}{4} = \frac{18+5}{4} = \frac{23}{4}$
The sum is $\frac{23}{4}$.
j. Add $\frac{8}{3}$ + $\frac{2}{7}$.
The denominators are 3 and 7. The LCM(3, 7) = 21.
Convert fractions to equivalent fractions with denominator 21:
$\frac{8}{3} = \frac{8 \times 7}{3 \times 7} = \frac{56}{21}$
$\frac{2}{7} = \frac{2 \times 3}{7 \times 3} = \frac{6}{21}$
Add the equivalent fractions:
$\frac{56}{21} + \frac{6}{21} = \frac{56+6}{21} = \frac{62}{21}$
The sum is $\frac{62}{21}$.
k. Add $\frac{3}{4}$ + $\frac{1}{3}$ + $\frac{1}{5}$.
This is the same addition problem as in part e.
The denominators are 4, 3, and 5. The LCM(4, 3, 5) = 60.
Equivalent fractions: $\frac{45}{60}$, $\frac{20}{60}$, $\frac{12}{60}$.
Add the equivalent fractions:
$\frac{45}{60} + \frac{20}{60} + \frac{12}{60} = \frac{45+20+12}{60} = \frac{77}{60}$
The sum is $\frac{77}{60}$.
l. Add $\frac{2}{3}$ + $\frac{4}{5}$ + $\frac{3}{7}$.
The denominators are 3, 5, and 7. The LCM(3, 5, 7) = $3 \times 5 \times 7 = 105$.
Convert fractions to equivalent fractions with denominator 105:
$\frac{2}{3} = \frac{2 \times 35}{3 \times 35} = \frac{70}{105}$
$\frac{4}{5} = \frac{4 \times 21}{5 \times 21} = \frac{84}{105}$
$\frac{3}{7} = \frac{3 \times 15}{7 \times 15} = \frac{45}{105}$
Add the equivalent fractions:
$\frac{70}{105} + \frac{84}{105} + \frac{45}{105} = \frac{70+84+45}{105} = \frac{199}{105}$
The sum is $\frac{199}{105}$.
m. Add $\frac{9}{2}$ + $\frac{5}{4}$ + $\frac{7}{6}$.
The denominators are 2, 4, and 6.
Find the LCM(2, 4, 6):
$\begin{array}{c|cc} 2 & 2 \;, & 4 \;, & 6 \\ \hline 2 & 1 \; , & 2 \; , & 3 \\ \hline 3 & 1 \; , & 1 \; , & 3 \\ \hline & 1 \; , & 1 \; , & 1 \end{array}$
LCM = $2 \times 2 \times 3 = 12$.
Convert fractions to equivalent fractions with denominator 12:
$\frac{9}{2} = \frac{9 \times 6}{2 \times 6} = \frac{54}{12}$
$\frac{5}{4} = \frac{5 \times 3}{4 \times 3} = \frac{15}{12}$
$\frac{7}{6} = \frac{7 \times 2}{6 \times 2} = \frac{14}{12}$
Add the equivalent fractions:
$\frac{54}{12} + \frac{15}{12} + \frac{14}{12} = \frac{54+15+14}{12} = \frac{83}{12}$
The sum is $\frac{83}{12}$.
Question 2. Rahim mixes $\frac{2}{3}$ litres of yellow paint with $\frac{3}{4}$ litres of blue paint to make green paint. What is the volume of green paint he has made?
Answer:
Given:
Volume of yellow paint = $\frac{2}{3}$ litres
Volume of blue paint = $\frac{3}{4}$ litres
To Find:
The total volume of green paint made.
Solution:
To find the total volume of green paint, we need to add the volume of yellow paint and the volume of blue paint.
Total volume = Volume of yellow paint + Volume of blue paint
Total volume = $\frac{2}{3} + \frac{3}{4}$
To add these fractions, we need to find a common denominator. The denominators are 3 and 4. The least common multiple (LCM) of 3 and 4 is 12.
Convert each fraction to an equivalent fraction with a denominator of 12:
$\frac{2}{3} = \frac{2 \times 4}{3 \times 4} = \frac{8}{12}$
$\frac{3}{4} = \frac{3 \times 3}{4 \times 3} = \frac{9}{12}$
Now, add the equivalent fractions:
Total volume = $\frac{8}{12} + \frac{9}{12}$
Add the numerators and keep the common denominator:
Total volume = $\frac{8 + 9}{12} = \frac{17}{12}$
The total volume of green paint made is $\frac{17}{12}$ litres.
This can also be expressed as a mixed number:
$\frac{17}{12} = 1 \frac{5}{12}$
Answer: Rahim has made $\frac{17}{12}$ litres (or $1 \frac{5}{12}$ litres) of green paint.
Question 3. Geeta bought $\frac{2}{5}$ meter of lace and Shamim bought $\frac{3}{4}$ meter of the same lace to put a complete border on a table cloth whose perimeter is 1 meter long. Find the total length of the lace they both have bought. Will the lace be sufficient to cover the whole border?
Answer:
Given:
Length of lace Geeta bought = $\frac{2}{5}$ meter
Length of lace Shamim bought = $\frac{3}{4}$ meter
Perimeter of the table cloth = 1 meter
To Find:
1. Total length of lace they both have bought.
2. Whether the lace is sufficient to cover the whole border.
Solution:
1. To find the total length of lace they both have bought, we need to add the length of lace Geeta bought and the length of lace Shamim bought.
Total length of lace = Length Geeta bought + Length Shamim bought
Total length of lace = $\frac{2}{5} + \frac{3}{4}$
To add these fractions, we need to find a common denominator. The denominators are 5 and 4. The least common multiple (LCM) of 5 and 4 is 20.
Convert each fraction to an equivalent fraction with a denominator of 20:
$\frac{2}{5} = \frac{2 \times 4}{5 \times 4} = \frac{8}{20}$
$\frac{3}{4} = \frac{3 \times 5}{4 \times 5} = \frac{15}{20}$
Now, add the equivalent fractions:
Total length of lace = $\frac{8}{20} + \frac{15}{20}$
Total length of lace = $\frac{8+15}{20} = \frac{23}{20}$ meters.
2. To determine if the lace is sufficient, we compare the total length of lace with the perimeter of the table cloth.
Total length of lace = $\frac{23}{20}$ meters
Perimeter of table cloth = 1 meter
We can write 1 meter as a fraction with denominator 20: $1 = \frac{20}{20}$.
Now compare $\frac{23}{20}$ and $\frac{20}{20}$.
Since the denominators are the same, we compare the numerators. $23 > 20$.
Therefore, $\frac{23}{20} > \frac{20}{20}$.
This means the total length of lace is greater than the perimeter of the table cloth.
So, the lace will be sufficient to cover the whole border.
Answer:
The total length of lace they both have bought is $\frac{23}{20}$ meters.
The lace will be sufficient to cover the whole border because $\frac{23}{20} \text{ meters} > 1 \text{ meter}$.
Figure it Out (Page 181)
Question 1. $\frac{5}{8}$ – $\frac{3}{8}$
Answer:
Given:
Subtraction problem: $\frac{5}{8} - \frac{3}{8}$
To Find:
The difference between the given fractions.
Solution:
The given fractions $\frac{5}{8}$ and $\frac{3}{8}$ have the same denominator, which is 8. These are like fractions.
To subtract like fractions, we subtract the numerators and keep the denominator the same.
$\frac{5}{8} - \frac{3}{8} = \frac{5 - 3}{8}$
Subtracting the numerators:
$5 - 3 = 2$
So, the difference is:
$\frac{2}{8}$
The resulting fraction can be simplified by dividing both the numerator and the denominator by their greatest common divisor (GCD).
The GCD of 2 and 8 is 2.
$\frac{2}{8} = \frac{2 \div 2}{8 \div 2} = \frac{1}{4}$
The difference is $\frac{1}{4}$.
Question 2. $\frac{7}{9}$ – $\frac{5}{9}$
Answer:
Given:
Subtraction problem: $\frac{7}{9} - \frac{5}{9}$
To Find:
The difference between the given fractions.
Solution:
The given fractions $\frac{7}{9}$ and $\frac{5}{9}$ have the same denominator, which is 9. These are like fractions.
To subtract like fractions, we subtract the numerators and keep the denominator the same.
$\frac{7}{9} - \frac{5}{9} = \frac{7 - 5}{9}$
Subtracting the numerators:
$7 - 5 = 2$
So, the difference is:
$\frac{2}{9}$
The fraction $\frac{2}{9}$ is already in its lowest terms because the greatest common divisor (GCD) of 2 and 9 is 1.
The difference is $\frac{2}{9}$.
Question 3. $\frac{10}{27}$ – $\frac{1}{27}$
Answer:
Given:
Subtraction problem: $\frac{10}{27} - \frac{1}{27}$
To Find:
The difference between the given fractions.
Solution:
The given fractions $\frac{10}{27}$ and $\frac{1}{27}$ have the same denominator, which is 27. These are like fractions.
To subtract like fractions, we subtract the numerators and keep the denominator the same.
$\frac{10}{27} - \frac{1}{27} = \frac{10 - 1}{27}$
Subtracting the numerators:
$10 - 1 = 9$
So, the difference is:
$\frac{9}{27}$
The resulting fraction can be simplified by dividing both the numerator and the denominator by their greatest common divisor (GCD).
The GCD of 9 and 27 is 9, since $27 = 3 \times 9$.
$\frac{9}{27} = \frac{9 \div 9}{27 \div 9} = \frac{1}{3}$
The difference is $\frac{1}{3}$.
Figure it Out (Page 182)
Question 1. Carry out the following subtractions using Brahmagupta’s method:
a. $\frac{8}{15}$ – $\frac{3}{15}$
b. $\frac{2}{5}$ – $\frac{4}{15}$
c. $\frac{5}{6}$ – $\frac{4}{9}$
d. $\frac{2}{3}$ – $\frac{1}{2}$
Answer:
Brahmagupta's method for subtracting $\frac{c}{d}$ from $\frac{a}{b}$ is given by $\frac{ad - bc}{bd}$. This is equivalent to finding a common denominator and subtracting the numerators. We will use the method of finding the least common multiple (LCM) of the denominators to perform the subtraction.
a. Subtract $\frac{3}{15}$ from $\frac{8}{15}$.
The fractions have the same denominator (15). These are like fractions.
Subtract the numerators and keep the common denominator:
$\frac{8}{15} - \frac{3}{15} = \frac{8-3}{15} = \frac{5}{15}$
Simplify the result by dividing the numerator and denominator by their GCD, which is 5:
$\frac{5}{15} = \frac{\cancel{5}^{1}}{\cancel{15}_{3}} = \frac{1}{3}$
The difference is $\frac{1}{3}$.
b. Subtract $\frac{4}{15}$ from $\frac{2}{5}$.
The denominators are 5 and 15. The LCM(5, 15) = 15.
Convert $\frac{2}{5}$ to an equivalent fraction with denominator 15:
$\frac{2}{5} = \frac{2 \times 3}{5 \times 3} = \frac{6}{15}$
The fraction $\frac{4}{15}$ already has the denominator 15.
Subtract the equivalent fractions:
$\frac{6}{15} - \frac{4}{15} = \frac{6-4}{15} = \frac{2}{15}$
The fraction $\frac{2}{15}$ is in its lowest terms as the GCD(2, 15) = 1.
The difference is $\frac{2}{15}$.
c. Subtract $\frac{4}{9}$ from $\frac{5}{6}$.
The denominators are 6 and 9. The LCM(6, 9) = 18.
Convert fractions to equivalent fractions with denominator 18:
$\frac{5}{6} = \frac{5 \times 3}{6 \times 3} = \frac{15}{18}$
$\frac{4}{9} = \frac{4 \times 2}{9 \times 2} = \frac{8}{18}$
Subtract the equivalent fractions:
$\frac{15}{18} - \frac{8}{18} = \frac{15-8}{18} = \frac{7}{18}$
The fraction $\frac{7}{18}$ is in its lowest terms as the GCD(7, 18) = 1.
The difference is $\frac{7}{18}$.
d. Subtract $\frac{1}{2}$ from $\frac{2}{3}$.
The denominators are 3 and 2. The LCM(3, 2) = 6.
Convert fractions to equivalent fractions with denominator 6:
$\frac{2}{3} = \frac{2 \times 2}{3 \times 2} = \frac{4}{6}$
$\frac{1}{2} = \frac{1 \times 3}{2 \times 3} = \frac{3}{6}$
Subtract the equivalent fractions:
$\frac{4}{6} - \frac{3}{6} = \frac{4-3}{6} = \frac{1}{6}$
The fraction $\frac{1}{6}$ is in its lowest terms as the GCD(1, 6) = 1.
The difference is $\frac{1}{6}$.
Question 2. Subtract as indicated:
a. $\frac{13}{4}$ from $\frac{10}{3}$
b. $\frac{18}{5}$ from $\frac{23}{3}$
c. $\frac{29}{7}$ from $\frac{45}{7}$
Answer:
To subtract fractions, we first find a common denominator if needed, then subtract the numerators and keep the common denominator.
a. Subtract $\frac{13}{4}$ from $\frac{10}{3}$. This means calculating $\frac{10}{3} - \frac{13}{4}$.
The denominators are 3 and 4. The least common multiple (LCM) of 3 and 4 is 12.
Convert fractions to equivalent fractions with denominator 12:
$\frac{10}{3} = \frac{10 \times 4}{3 \times 4} = \frac{40}{12}$
$\frac{13}{4} = \frac{13 \times 3}{4 \times 3} = \frac{39}{12}$
Now subtract the equivalent fractions:
$\frac{40}{12} - \frac{39}{12} = \frac{40 - 39}{12} = \frac{1}{12}$
The difference is $\frac{1}{12}$.
b. Subtract $\frac{18}{5}$ from $\frac{23}{3}$. This means calculating $\frac{23}{3} - \frac{18}{5}$.
The denominators are 3 and 5. The LCM of 3 and 5 is 15.
Convert fractions to equivalent fractions with denominator 15:
$\frac{23}{3} = \frac{23 \times 5}{3 \times 5} = \frac{115}{15}$
$\frac{18}{5} = \frac{18 \times 3}{5 \times 3} = \frac{54}{15}$
Now subtract the equivalent fractions:
$\frac{115}{15} - \frac{54}{15} = \frac{115 - 54}{15}$
Performing the subtraction:
$\begin{array}{cc} & 1 & 1 & 5 \\ - & & 5 & 4 \\ \hline & & 6 & 1 \\ \hline \end{array}$
The difference is $\frac{61}{15}$.
c. Subtract $\frac{29}{7}$ from $\frac{45}{7}$. This means calculating $\frac{45}{7} - \frac{29}{7}$.
The fractions have the same denominator (7). These are like fractions.
Subtract the numerators and keep the common denominator:
$\frac{45}{7} - \frac{29}{7} = \frac{45 - 29}{7}$
Performing the subtraction:
$\begin{array}{cc} & 4 & 5 \\ - & 2 & 9 \\ \hline & 1 & 6 \\ \hline \end{array}$
The difference is $\frac{16}{7}$.
Question 3. Solve the following problems:
a. Jaya’s school is $\frac{7}{10}$ km from her home. She takes an auto for $\frac{1}{2}$ km from her home daily, and then walks the remaining distance to reach her school. How much does she walk daily to reach the school?
b. Jeevika takes $\frac{10}{3}$ minutes to take a complete round of the park and her friend Namit takes $\frac{13}{4}$ minutes to do the same. Who takes less time and by how much?
Answer:
a.
Given:
Total distance to school = $\frac{7}{10}$ km
Distance covered by auto = $\frac{1}{2}$ km
To Find:
The distance Jaya walks daily.
Solution:
The distance Jaya walks is the total distance minus the distance covered by auto.
Distance walked = Total distance - Distance by auto
Distance walked = $\frac{7}{10} - \frac{1}{2}$
To subtract these fractions, we need a common denominator. The denominators are 10 and 2. The least common multiple (LCM) of 10 and 2 is 10.
Convert $\frac{1}{2}$ to an equivalent fraction with denominator 10:
$\frac{1}{2} = \frac{1 \times 5}{2 \times 5} = \frac{5}{10}$
Now, perform the subtraction:
Distance walked = $\frac{7}{10} - \frac{5}{10} = \frac{7 - 5}{10} = \frac{2}{10}$
Simplify the result:
$\frac{2}{10} = \frac{\cancel{2}^{1}}{\cancel{10}_{5}} = \frac{1}{5}$
Jaya walks $\frac{1}{5}$ km daily to reach the school.
Answer: Jaya walks $\frac{1}{5}$ km daily.
b.
Given:
Jeevika's time = $\frac{10}{3}$ minutes
Namit's time = $\frac{13}{4}$ minutes
To Find:
Who takes less time and by how much.
Solution:
To find who takes less time, we need to compare the two fractions $\frac{10}{3}$ and $\frac{13}{4}$.
To compare these fractions, we find a common denominator. The denominators are 3 and 4. The least common multiple (LCM) of 3 and 4 is 12.
Convert both fractions to equivalent fractions with denominator 12:
Jeevika's time: $\frac{10}{3} = \frac{10 \times 4}{3 \times 4} = \frac{40}{12}$ minutes
Namit's time: $\frac{13}{4} = \frac{13 \times 3}{4 \times 3} = \frac{39}{12}$ minutes
Now compare the equivalent fractions $\frac{40}{12}$ and $\frac{39}{12}$. Since the denominators are the same, we compare the numerators: $40 > 39$.
So, $\frac{40}{12} > \frac{39}{12}$. This means $\frac{10}{3} > \frac{13}{4}$.
Namit takes less time than Jeevika.
To find out by how much less time Namit takes, we subtract Namit's time from Jeevika's time:
Difference in time = Jeevika's time - Namit's time
Difference in time = $\frac{10}{3} - \frac{13}{4}$
We already converted these fractions to have a common denominator of 12:
Difference in time = $\frac{40}{12} - \frac{39}{12} = \frac{40 - 39}{12} = \frac{1}{12}$ minutes.
Namit takes $\frac{1}{12}$ minutes less than Jeevika.
Answer: Namit takes less time by $\frac{1}{12}$ minutes.
Intext Question (Page 184 - 185)
Question: Puzzle!
It is easy to add up fractional units to obtain the sum 1, if one uses the same fractional unit, e.g.,
$\frac{1}{2}$ + $\frac{1}{2}$ = 1, $\frac{1}{3}$ + $\frac{1}{3}$ + $\frac{1}{3}$ = 1, $\frac{1}{4}$ + $\frac{1}{4}$ + $\frac{1}{4}$ + $\frac{1}{4}$ = 1, etc.
1. Can you find three different fractional units that add up to 1?
It turns out there is only one solution to this problem (up to changing the order of the 3 fractions)! Can you find it? Try to find it before reading further.
2. Can you find four different fractional units that add up to 1?
It turns out that this problem has six solutions! Can you find at least one of them? Can you find them all? You can try using similar reasoning as in the cases of two and three fractional units – or find your own method!
Answer:
This puzzle asks us to find combinations of different unit fractions that add up to 1.
A unit fraction is a fraction where the numerator is 1 and the denominator is a positive integer, like $\frac{1}{2}$, $\frac{1}{3}$, $\frac{1}{4}$, etc.
Part 1: Three different fractional units that add up to 1.
We are looking for three distinct positive integers $a, b, c$ such that $\frac{1}{a} + \frac{1}{b} + \frac{1}{c} = 1$. Let's assume, without loss of generality, that $a < b < c$.
Consider the smallest possible integer value for $a$.
If $a = 1$, then $\frac{1}{1} + \frac{1}{b} + \frac{1}{c} = 1$. This means $1 + \frac{1}{b} + \frac{1}{c} = 1$, which simplifies to $\frac{1}{b} + \frac{1}{c} = 0$. Since $b$ and $c$ must be positive integers, $\frac{1}{b}$ and $\frac{1}{c}$ are positive, and their sum cannot be 0. So, $a$ cannot be 1.
If $a = 2$, then $\frac{1}{2} + \frac{1}{b} + \frac{1}{c} = 1$. Subtracting $\frac{1}{2}$ from both sides gives $\frac{1}{b} + \frac{1}{c} = 1 - \frac{1}{2} = \frac{1}{2}$.
We need to find distinct integers $b$ and $c$ such that $\frac{1}{b} + \frac{1}{c} = \frac{1}{2}$ and $a < b < c$, which means $2 < b < c$.
Since $b < c$, we have $\frac{1}{b} > \frac{1}{c}$. So, $\frac{1}{2} = \frac{1}{b} + \frac{1}{c} < \frac{1}{b} + \frac{1}{b} = \frac{2}{b}$.
This inequality $\frac{1}{2} < \frac{2}{b}$ implies $b < 4$.
Since we require $2 < b < c$, the only possible integer value for $b$ that satisfies $2 < b < 4$ is $b = 3$.
Substitute $b=3$ into the equation $\frac{1}{b} + \frac{1}{c} = \frac{1}{2}$:
$\frac{1}{3} + \frac{1}{c} = \frac{1}{2}$
Subtract $\frac{1}{3}$ from both sides:
$\frac{1}{c} = \frac{1}{2} - \frac{1}{3} = \frac{3}{6} - \frac{2}{6} = \frac{1}{6}$
So, $c = 6$.
The three fractional units are $\frac{1}{2}$, $\frac{1}{3}$, and $\frac{1}{6}$. They are distinct, and $2 < 3 < 6$. Let's check their sum:
$\frac{1}{2} + \frac{1}{3} + \frac{1}{6} = \frac{3}{6} + \frac{2}{6} + \frac{1}{6} = \frac{3+2+1}{6} = \frac{6}{6} = 1$.
This confirms that these three fractional units add up to 1.
If $a \ge 3$, then $\frac{1}{a} \le \frac{1}{3}$. Since $a < b < c$, we would have $\frac{1}{b} < \frac{1}{3}$ and $\frac{1}{c} < \frac{1}{3}$. The sum $\frac{1}{a} + \frac{1}{b} + \frac{1}{c} \le \frac{1}{3} + \frac{1}{4} + \frac{1}{5} = \frac{20+15+12}{60} = \frac{47}{60}$. Since $\frac{47}{60} < 1$, it's impossible to reach 1 if $a \ge 3$ with distinct denominators.
Thus, the only set of three different fractional units that add up to 1 is $\frac{1}{2}, \frac{1}{3}, \frac{1}{6}$.
Part 2: Four different fractional units that add up to 1.
We are looking for four distinct positive integers $a, b, c, d$ such that $\frac{1}{a} + \frac{1}{b} + \frac{1}{c} + \frac{1}{d} = 1$. Let's assume $a < b < c < d$.
Consider the smallest possible integer value for $a$.
If $a = 1$, then $\frac{1}{1} + \frac{1}{b} + \frac{1}{c} + \frac{1}{d} = 1$, which implies $\frac{1}{b} + \frac{1}{c} + \frac{1}{d} = 0$. This is impossible for positive integers $b, c, d$. So, $a$ cannot be 1.
If $a = 2$, then $\frac{1}{2} + \frac{1}{b} + \frac{1}{c} + \frac{1}{d} = 1$. This implies $\frac{1}{b} + \frac{1}{c} + \frac{1}{d} = \frac{1}{2}$.
We need $2 < b < c < d$. Since $b < c < d$, we have $\frac{1}{b} > \frac{1}{c} > \frac{1}{d}$.
$\frac{1}{2} = \frac{1}{b} + \frac{1}{c} + \frac{1}{d} < \frac{1}{b} + \frac{1}{b} + \frac{1}{b} = \frac{3}{b}$.
This inequality $\frac{1}{2} < \frac{3}{b}$ implies $b < 6$.
Since $b > a = 2$, the possible integer values for $b$ are $\{3, 4, 5\}$.
Case $a=2, b=3$: $\frac{1}{3} + \frac{1}{c} + \frac{1}{d} = \frac{1}{2}$. This means $\frac{1}{c} + \frac{1}{d} = \frac{1}{2} - \frac{1}{3} = \frac{1}{6}$.
We need $3 < c < d$. Since $c < d$, $\frac{1}{c} > \frac{1}{d}$.
$\frac{1}{6} = \frac{1}{c} + \frac{1}{d} < \frac{1}{c} + \frac{1}{c} = \frac{2}{c} \implies c < 12$.
Also, $\frac{1}{c} < \frac{1}{6} \implies c > 6$.
So, possible integer values for $c$ are $\{7, 8, 9, 10, 11\}$. We test each:
- If $c=7$: $\frac{1}{7} + \frac{1}{d} = \frac{1}{6} \implies \frac{1}{d} = \frac{1}{6} - \frac{1}{7} = \frac{7-6}{42} = \frac{1}{42}$. So $d=42$. Solution: $\{\frac{1}{2}, \frac{1}{3}, \frac{1}{7}, \frac{1}{42}\}$. $2<3<7<42$. Valid.
- If $c=8$: $\frac{1}{8} + \frac{1}{d} = \frac{1}{6} \implies \frac{1}{d} = \frac{1}{6} - \frac{1}{8} = \frac{4-3}{24} = \frac{1}{24}$. So $d=24$. Solution: $\{\frac{1}{2}, \frac{1}{3}, \frac{1}{8}, \frac{1}{24}\}$. $2<3<8<24$. Valid.
- If $c=9$: $\frac{1}{9} + \frac{1}{d} = \frac{1}{6} \implies \frac{1}{d} = \frac{1}{6} - \frac{1}{9} = \frac{3-2}{18} = \frac{1}{18}$. So $d=18$. Solution: $\{\frac{1}{2}, \frac{1}{3}, \frac{1}{9}, \frac{1}{18}\}$. $2<3<9<18$. Valid.
- If $c=10$: $\frac{1}{10} + \frac{1}{d} = \frac{1}{6} \implies \frac{1}{d} = \frac{1}{6} - \frac{1}{10} = \frac{5-3}{30} = \frac{2}{30} = \frac{1}{15}$. So $d=15$. Solution: $\{\frac{1}{2}, \frac{1}{3}, \frac{1}{10}, \frac{1}{15}\}$. $2<3<10<15$. Valid.
- If $c=11$: $\frac{1}{11} + \frac{1}{d} = \frac{1}{6} \implies \frac{1}{d} = \frac{1}{6} - \frac{1}{11} = \frac{11-6}{66} = \frac{5}{66}$. $d = \frac{66}{5}$, not an integer.
Case $a=2, b=4$: $\frac{1}{4} + \frac{1}{c} + \frac{1}{d} = \frac{1}{2}$. This means $\frac{1}{c} + \frac{1}{d} = \frac{1}{2} - \frac{1}{4} = \frac{1}{4}$.
We need $4 < c < d$. Since $c < d$, $\frac{1}{c} > \frac{1}{d}$.
$\frac{1}{4} = \frac{1}{c} + \frac{1}{d} < \frac{1}{c} + \frac{1}{c} = \frac{2}{c} \implies c < 8$.
Also, $\frac{1}{c} < \frac{1}{4} \implies c > 4$.
So, possible integer values for $c$ are $\{5, 6, 7\}$. We test each:
- If $c=5$: $\frac{1}{5} + \frac{1}{d} = \frac{1}{4} \implies \frac{1}{d} = \frac{1}{4} - \frac{1}{5} = \frac{5-4}{20} = \frac{1}{20}$. So $d=20$. Solution: $\{\frac{1}{2}, \frac{1}{4}, \frac{1}{5}, \frac{1}{20}\}$. $2<4<5<20$. Valid.
- If $c=6$: $\frac{1}{6} + \frac{1}{d} = \frac{1}{4} \implies \frac{1}{d} = \frac{1}{4} - \frac{1}{6} = \frac{3-2}{12} = \frac{1}{12}$. So $d=12$. Solution: $\{\frac{1}{2}, \frac{1}{4}, \frac{1}{6}, \frac{1}{12}\}$. $2<4<6<12$. Valid.
- If $c=7$: $\frac{1}{7} + \frac{1}{d} = \frac{1}{4} \implies \frac{1}{d} = \frac{1}{4} - \frac{1}{7} = \frac{7-4}{28} = \frac{3}{28}$. $d = \frac{28}{3}$, not an integer.
Case $a=2, b=5$: $\frac{1}{5} + \frac{1}{c} + \frac{1}{d} = \frac{1}{2}$. This means $\frac{1}{c} + \frac{1}{d} = \frac{1}{2} - \frac{1}{5} = \frac{3}{10}$.
We need $5 < c < d$. Since $c < d$, $\frac{1}{c} > \frac{1}{d}$.
$\frac{3}{10} = \frac{1}{c} + \frac{1}{d} < \frac{1}{c} + \frac{1}{c} = \frac{2}{c} \implies 3c < 20$, $c < 6.66\dots$.
Also, $\frac{1}{c} < \frac{3}{10} \implies c > \frac{10}{3} = 3.33\dots$.
So, possible integer values for $c$ satisfying $5 < c < 6.66\dots$ are none.
Let's recheck the bound $\frac{1}{c} < \frac{3}{10}$. Yes, $c$ must be greater than $10/3$. We also need $b < c$, so $5 < c$. Possible integer values for $c$ are $c=6$. If $c=6$: $\frac{1}{6} + \frac{1}{d} = \frac{3}{10} \implies \frac{1}{d} = \frac{3}{10} - \frac{1}{6} = \frac{9-5}{30} = \frac{4}{30} = \frac{2}{15}$. $d = \frac{15}{2}$, not an integer.
If $a \ge 3$, then $\frac{1}{a} \le \frac{1}{3}$. Since $a < b < c < d$, we have $\frac{1}{b} < \frac{1}{3}$, $\frac{1}{c} < \frac{1}{3}$, $\frac{1}{d} < \frac{1}{3}$. The sum $\frac{1}{a} + \frac{1}{b} + \frac{1}{c} + \frac{1}{d} \le \frac{1}{3} + \frac{1}{4} + \frac{1}{5} + \frac{1}{6} = \frac{20+15+12+10}{60} = \frac{57}{60}$. Since $\frac{57}{60} < 1$, it's impossible to reach 1 if $a \ge 3$ with distinct denominators.
The six sets of four different fractional units that add up to 1 are (listing the denominators in ascending order):
- $\{2, 3, 7, 42\}$ i.e., $\frac{1}{2} + \frac{1}{3} + \frac{1}{7} + \frac{1}{42} = 1$
- $\{2, 3, 8, 24\}$ i.e., $\frac{1}{2} + \frac{1}{3} + \frac{1}{8} + \frac{1}{24} = 1$
- $\{2, 3, 9, 18\}$ i.e., $\frac{1}{2} + \frac{1}{3} + \frac{1}{9} + \frac{1}{18} = 1$
- $\{2, 3, 10, 15\}$ i.e., $\frac{1}{2} + \frac{1}{3} + \frac{1}{10} + \frac{1}{15} = 1$
- $\{2, 4, 5, 20\}$ i.e., $\frac{1}{2} + \frac{1}{4} + \frac{1}{5} + \frac{1}{20} = 1$
- $\{2, 4, 6, 12\}$ i.e., $\frac{1}{2} + \frac{1}{4} + \frac{1}{6} + \frac{1}{12} = 1$

